通过前面系列文章的介绍,基本可以掌握离散傅立叶变换算法的计算和执行过程,并清楚地知道快速傅立叶变换的执行过程以及它快的原因。下面开始介绍三维海面渲染的过程。
本篇文章作为这个系列的结尾。会重点讲解海面渲染的流程,并且会引用我在学习这部分内容时参考的开源代码和两篇文章。我会将论文作为辅助资料,重点讲解开源代码的内容。希望可以带着大家利用前面学习的知识,一步步实现海面渲染。
这里只重点讲解如何生成高度偏移贴图、水平偏移贴图和法线贴图的生成。有一些比较难懂的数学公式,因为作者能力有限,只做摘抄,不做详细讲解。对于海面网格的生成,LOD部分不做详细介绍,如果大家有兴趣,可以多多点赞,我另外写一篇文章讲解这个内容。
海面渲染的一般步骤
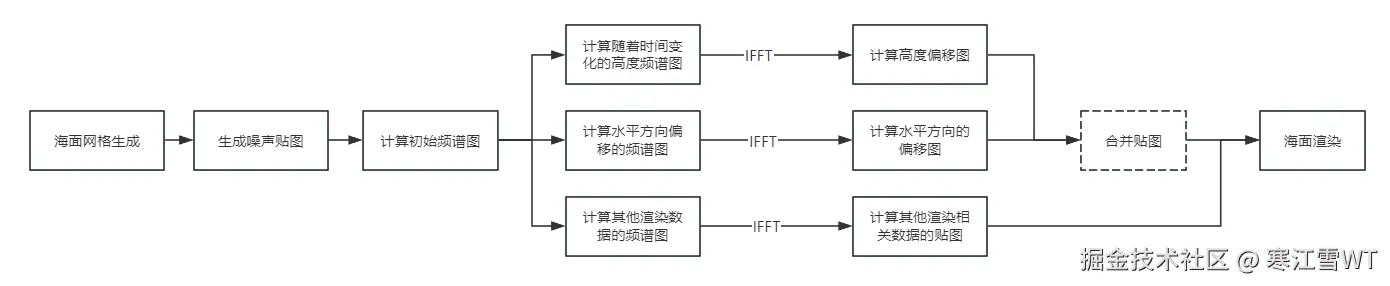
上面的流程图,就表示了还面渲染的一般流程。其中,海面网格生成,噪声贴图和初始频谱的生成都可以在初始化时计算出来。如果风向,风速等初始参数没有变化,初始频谱不用每一帧都更新。而每一帧的更新,要需要更新高度偏移的频谱图、水平方向偏移的频谱图以及其他频谱图,例如法线、湍流程度的计算等等。后续会根据开源代码一一介绍。
初始频谱的公式有很多,例如网上能直接搜到的Phillips频谱公式,Jonswap频谱公式在一篇论文中,中文互联网似乎搜不到,但我所要分析的源码是实现了这篇论文的内容的。下面先简单介绍Phillips频谱公式及基于该公式的海面模拟过程但不会详细介绍,随后结合开源代码介绍Jonswap频谱公式及与之相关的海面模拟过程。
基于Phillips频谱的海面模拟
初始化频谱$h_0(\vec{k})$和$h_0^*(\vec{k})$
在论文[1]中详细介绍了Phillips频谱公式。下面给出公式的具体计算方法,及相关参数的计算。在后文中给出解释。
上面的式子中。$A$是一个浮点数常数,$L’$是海面的长度,也是一个浮点数,$V$是指风速,也是一个浮点数常数,$g$是重力加速度,值为9.81。$N$是贴图的分辨率,这里无论是频谱贴图还是最后生成的高度图,都使用统一的分辨率。$n,m$是一组在-$N/2$到$N/2$之间的整数,在实际计算中,ComputeShader的ThreadID就是一个$0-N$的整数,分别减去$N/2$即可得到$n$和$m$。代入计算可以计算出$\vec{k}$。$\vec{w}$是由$\vec{k}$计算所得,公式如上。随后所有的参数代入Phillips频谱公式中。
不过这还没结束。函数$P_h(\vec{k})$计算得到的浮点数还不能作为初始频谱,还要经过下面的计算才行。
这里$\varepsilon_r$和$\varepsilon_i$是两个独立的服从标准正太分布的浮点数,可以从预先生成的噪声贴图中采样得到,然后凑成一个复数,按复数的计算公式进行展开,这很简单。随后将该复数乘以Phillips频率公式计算得到的值,但是要做一些变化,跟着公式进行就好。这样就可以计算出$h_0(\vec{k})$了,同时计算了它反方向的频率,$h_0^*(\vec{k})$。这样得到的两个复数,可以存在同一张贴图里。
论文中的附件给出了相应的ComputeShader实现,可以参考作者的实现来理解。
瞬时频谱$h(\vec{k},t)$的生成
有了$h_0(\vec{k})$和$h_0^*(\vec{k})$之后,就要基于这两个初始值,计算在某一个时刻的频谱,这样才可以获得在时间上连续的频谱。计算公式如下:
这里的公式引入了$\exp(i\omega(k)t)$,这里可以用欧拉公式展开,展开式如下:
很明显,这是个复数,而先前计算的$h_0$和$h_0^*$也是复数,这里按复数乘法来进行计算乘积和求和即可计算出$h(\vec{k},t)$,这里计算结果也是复数,保存在贴图里,作为IFFT的输入。
IFFT过程
快速逆傅里叶逆变换的过程可以迅速地将前面计算得到的频谱图,计算出高度偏移的值。而IFFT的计算过程,可以称作蝶形变换。不过我这里不想直接贴蝶形变换的图,而是从整个递归过程及$W_N^k$的周期性来解释这个加速的原理,然后再解释蝶形变换,也是为了填第三篇挖的坑。
首先来讲周期性,即$W_N^k$有这样一个性质:
在第三篇中,介绍了傅里叶变换过程中,递归公式展开后的形式如下图:
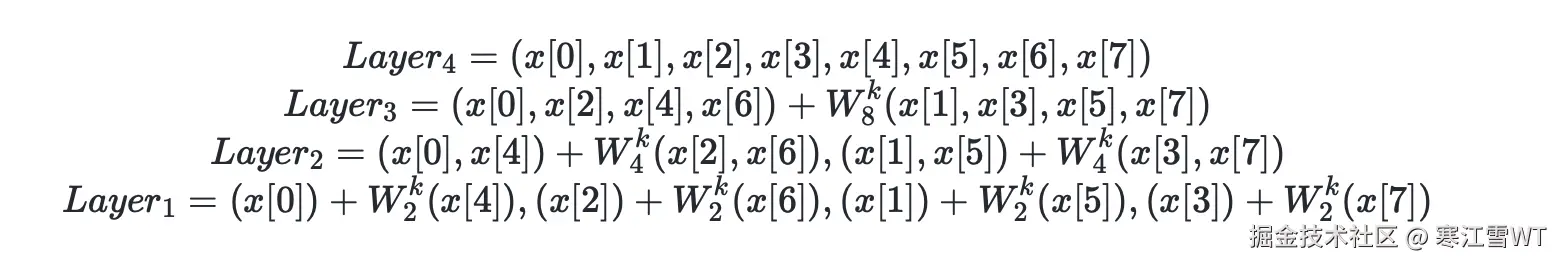
结合周期性来看上面这张图,如果按顺序每个$X[i]$去计算右边的乘积及求和。会发现这样一种情况,在计算$X[0],X[2],X[4],X[6]$时,$x[4],x[5],x[6],x[7]$这一项的乘积是相等的,这是因为$W_2^0=W_2^2=W_2^4=W_2^6$。同理可以推出在计算$X[1],X[3],X[5],X[7]$时,$x[4],x[5],x[6],x[7]$这一项也是是相等的,这是因为$W_2^1=W_2^3=W_2^5=W_2^7$。所以可以很轻松地得到一个结论:在整个计算过程中,$x[4]W_2^0,x[5]W_2^0,x[6]W_2^0,x[7]W_2^0$和$x[4]W_2^1,x[5]W_2^1,x[6]W_2^1,x[7]W_2^1$只需要计算一次即可。同理可以验证$W_4^k$和$W_8^k$的结论,这里$W_N^k$的周期性是加速的基本条件。
所以蝶形变换的本质就是为每个$x[i]$在凑上面的和式,且不用重复计算。8个数的FFT蝶形变换的过程,可以表示成下面这张图。这里重叠的线条比较多,并不直观。我用PPT把这个过程做成动画,放在附件里。
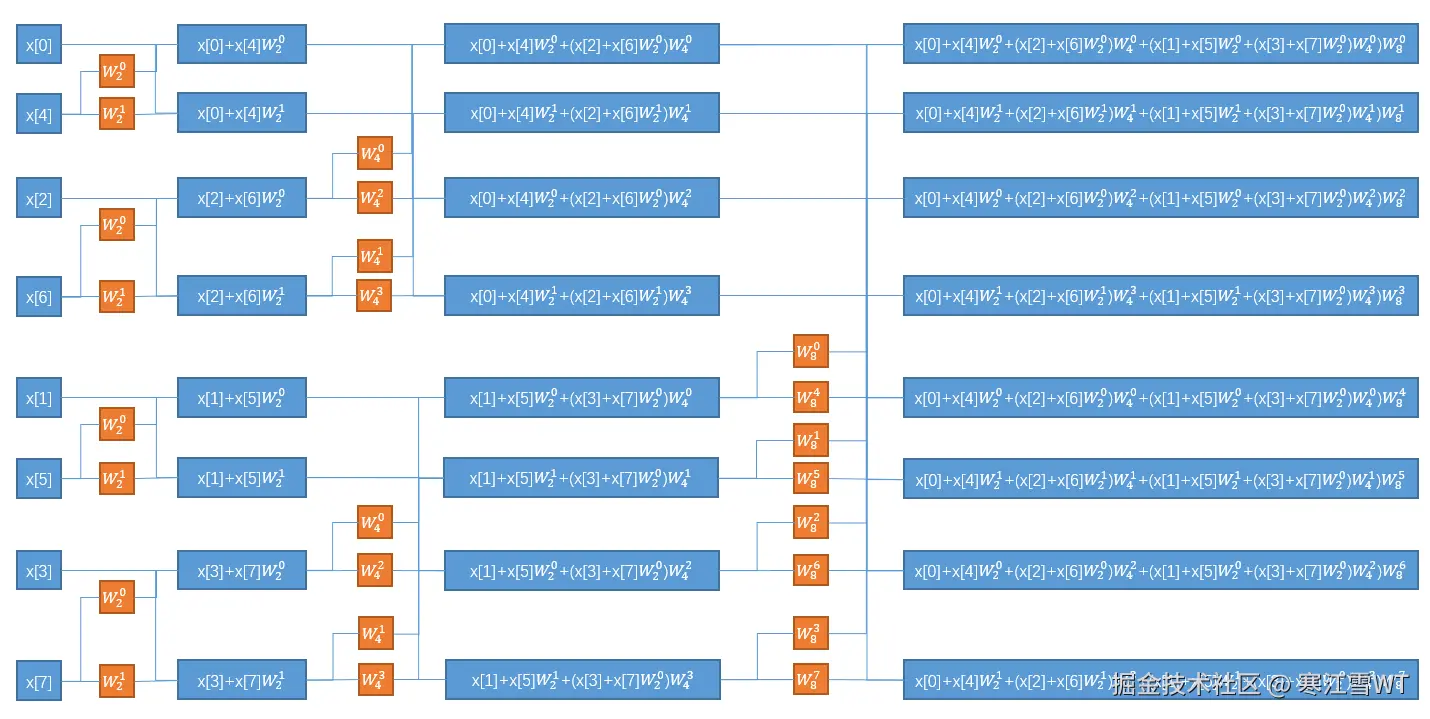
可以看到,蝶形变换的过程,每一轮递进就是在用上一轮计算的结果(包括输入的数组序列),乘以常数$W_N^k$,然后进行相加。既然是常数,而且是利用上一轮计算的结果。那么就可以预计算出每一轮递进过程中要使用的常数$W_N^k$以及进行组合的索引。在论文[1]中,将预计算的结果保存成贴图,叫做”Butterfly Texture”,论文中还总结了计算规律。Butterfly Texture的尺寸是$log(N)\times N$,如下图所示,是一张8x256的Butterfly Texture。

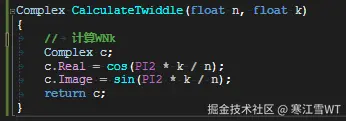
下面这段代码给出了$W_N^k$的计算过程。Comlex是复数类类型,即$Real + Image*i$的形式。加减乘除均按复数的计算规则进行计算。
下面的代码给出了”Butterfly Texture”的生成步骤,在ComputeShader中计算。注释中写明了每一行的含义。
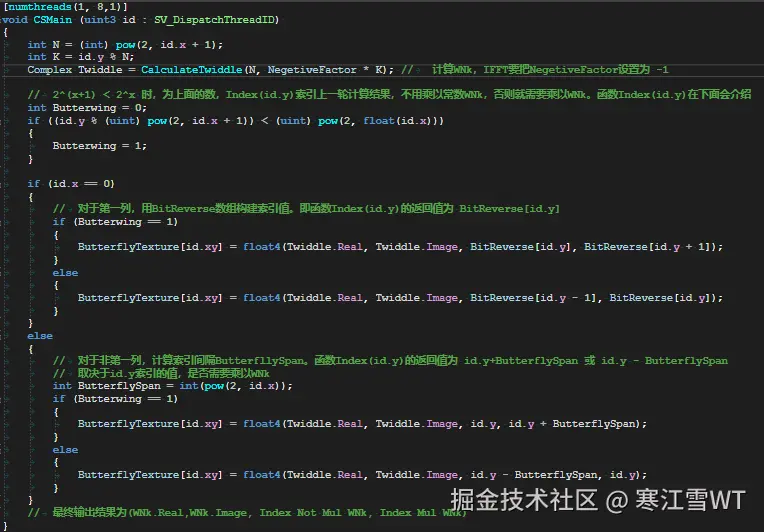
有了”Butterfly Texture”之后,接下来就是要看怎么用它来做FFT或IFFT了。关于海洋模拟,用到的是IFFT,不过这里介绍FFT就可以知道IFFT怎么做了。前面有介绍过,二维的FFT要先进行一次一维的FFT,然后再按列进行一次一维的FFT。对于一张NxN的贴图,在每一次变换时,需要执行 $log N$次ComputeShader,横向和纵向变换总共执行$2logN$次。这里引入了两张”PingPong Texture”,用于在两次执行时,互相切换着作为输入和输出。
下面是FFT横向变换的代码,写满了注释,可以参考着看。
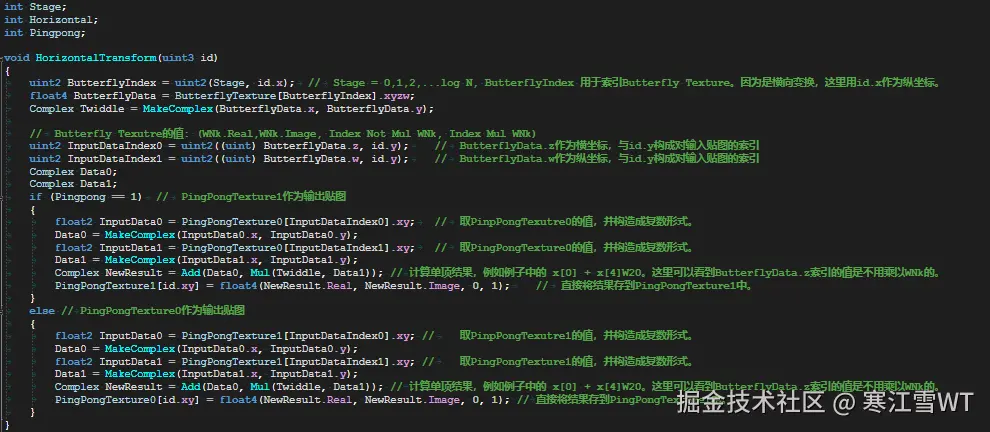
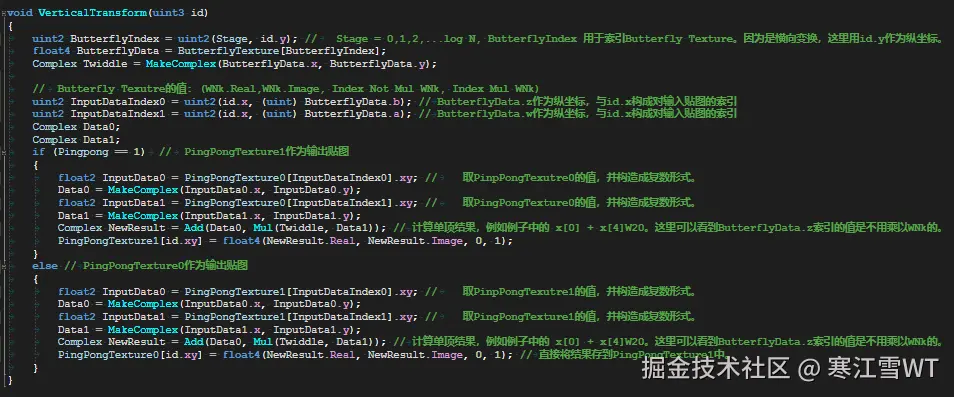
下面是FFT纵向变换的代码,也写满了注释,可以参考着看。
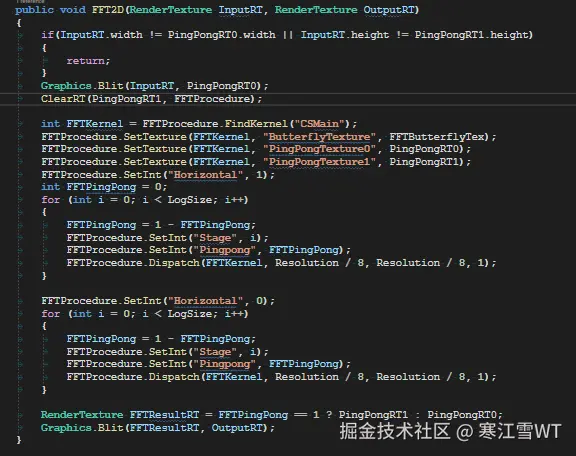
下面是C#中调用ComputeShader的代码。核心代码在两个For循环之内,就不解释了。
这里给出的是FFT的过程,实际上IFFT也没有什么不同。如果是要还原图像的话,IFFT的结果要统一除以一个NxN。在做海面时,如果除以NxN,得到的偏移幅度会很小,可以不除以NxN。
对IFFT的结果进行置换
IFFT得到的结果已经算高度上的偏移。这里文章没有介绍原因,只给出了计算过程。过程很简单。就是根据坐标的奇偶性来决定是否在正上方还是下方。在测试时发现,没有这个操作,海面的起伏的高度差很小,看起来变化非常迅速。

计算高度偏移贴图
在瞬时频谱$h(\vec{k},t)$生成之后,直接执行IFFT可以得到高度偏移贴图,这里就没什么难度了。

这里高度偏移贴图会在渲染海面网格时,在顶点着色器中采样,并对顶点进行偏移。
海面网格的生成及其LOD
海面网格用的是四叉树进行快速构建,并且在距离中心位置很远的位置,取更高层级的四叉树节点,这样在距离中心位置远的位置,网格点更少,提高渲染效率。在不同的LOD网格之间,做衔接处理,如下图中,红色方框的位置,高层级的LOD网格中心点,向低层级的网格点细分出更多的三角形,这样在对顶点进行偏移时,在衔接处便不会破裂。理论上,用索引邻接网格顶点的方式,网格衔接处的顶点可以再减少一部分。四叉树这部分内容可以单独开一篇文章来讲解,就不在这里介绍了。

无限远的海面网格生成
在实际的应用中,海面网格会始终在海平面上跟着主角移动,使主角始终在海面网格中心的位置。即海面网格的Y轴坐标始终保持一致,只是在水平面上跟随主角X,Z轴的坐标。这样当主角的高度增加时,或者处于高出时,当视距无限远时,便会看到破绽。因此需要从边缘处向“无穷远”的位置生成三角面,用来保证在视线范围内,海平面不会穿帮。在公开的资料中,这通常被称为Skirt-Mesh,不知道应该如何翻译和理解。这里就只介绍生成的方法。
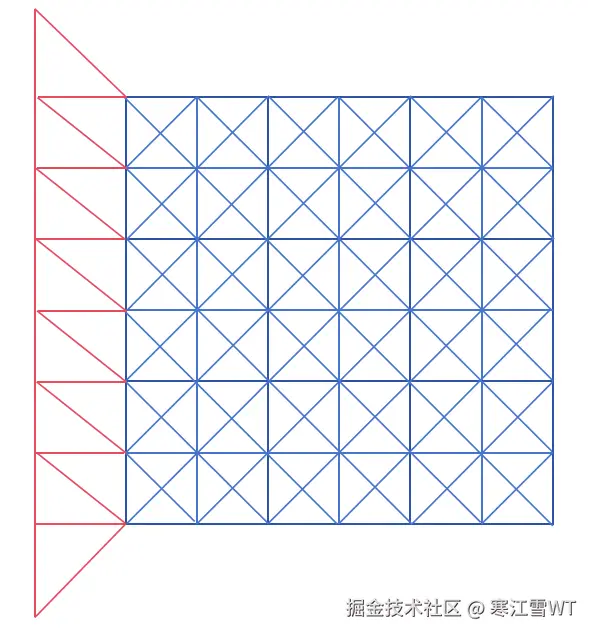
这里以左边的网格生成为例,其他方向的可以依次类推。可以看到,要生成的网格是一个梯形的形状,分为上下两个角点,右边的近点以及左边的远点,远点和角点在一条直线上,且远点和近点一 一对应,远点和角点的距离,就是我们说的“无限远”的距离,即一个很大很大的浮点数,这个数可以随意指定,也可以通过参数控制,这个在最后介绍。
这里近点很容易获得,然后就是生成远点和角点,在获得”无限远”距离之后,分别沿着下图中绿色箭头的方向计算出角点和远点即可。
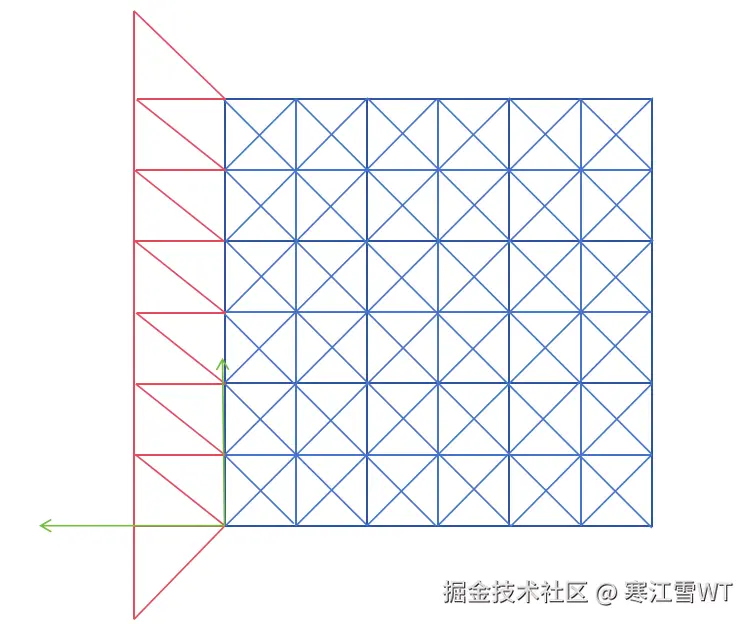
然后对它们进行编号。如下图所示,从下角点为0开始,一直往上编,使得远点的编号保持为奇数,近点的编号为偶数。
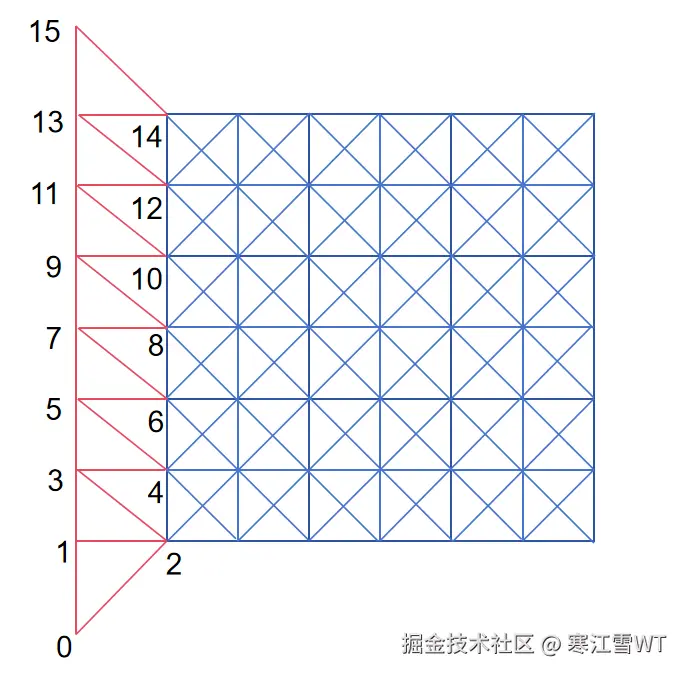
最后对它们进行三角化,生成顶点索引。下面是生成顶点索引的伪代码,按索引值的奇偶来决定该如何连接顶点。
for i from 0 to Vertices.Length - 2
if i % 2 == 0
Indices.Add(i,i+1,i+2)
else
Indices.Add(i,i+2,i+1)
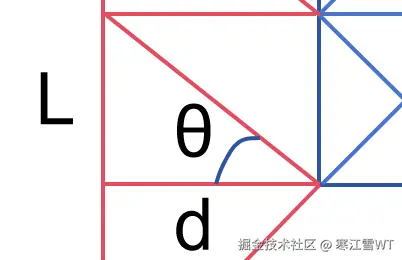
在本节末尾,介绍如何计算“无限远”的距离。这里有一个约束,就是两对远点和近点说构成的形状一定是矩形,如下图所示,绿框区域一定是矩形。这样的网格均匀且美观。
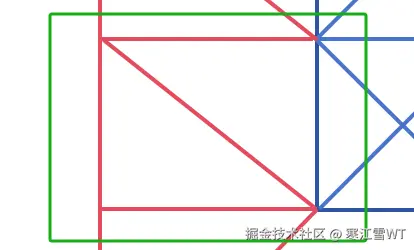
接着引入一个夹角,用来计算矩形的底边的长度,如下图所示,当夹角非常小时,$d = \frac{L}{tan(\theta)}$就会非常大,当距离非常大的时候,斜边看起来就像一条直线。
渲染
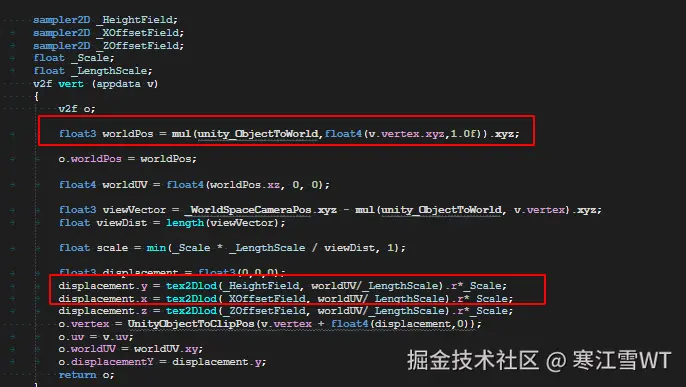
有了高度偏移贴图,海面网格之后。就要对网格的顶点进行偏移,这里是在顶点着色器中进行。计算出顶点的世界空间坐标,并除以LengthScale。这里的LengthScale就是前面计算初始频谱时的常数$L’$。因此海面网格的顶点扰动,是跟顶点的世界位置有关,也就是说,这张网格在空间中无论在任何位置,都可以采样这张偏移贴图。水平位移同理。
下面张图是一个不带渲染的实现效果,且没有Skirt-Mesh和LOD,可以看到顶点扰动的结果。Phillips的海面模拟,在第一次尝试时并不熟悉,所以得到的结果也不太自然。最后一篇文章将会介绍Jonswap频谱的效果,该实现公式较多,请给我一点时间整理。

参考文献
[1] Realtime GPGPU FFT Ocean Water Simulation
