RVO2相关算法的提出是来自这篇文章:《Reciprocal Collision Avoidance and Multi-Agent Navigation for Video Games》
RVO2的官方代码可以在这里下载到:https://gamma.cs.unc.edu/RVO2/publications/
该算法基于速度障碍域,计算单个agent的避免碰撞的移动速度或者移动方向。算法证明是正确的,但在实践中,仍然需要解决一些该算法本身没有考虑到的问题。
本文将介绍算法原理和存在的问题,以及解决方案。
RVO2算法原理介绍
假设有 A、B 两个运动中的圆形物体,如下图所示。
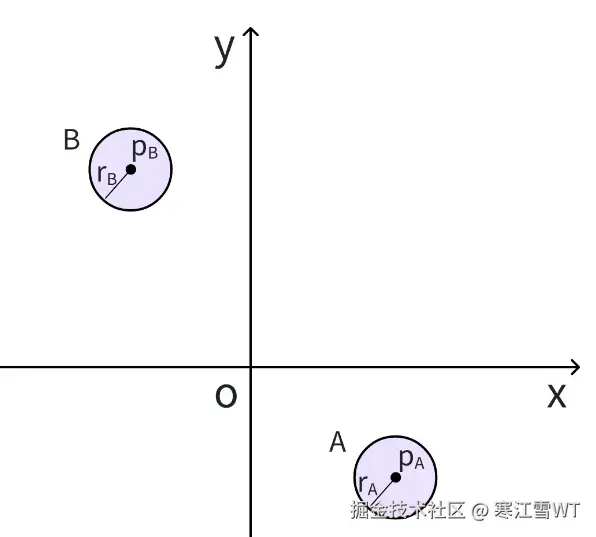
为了判断下一时间点能不能相撞,可以简化一下上面的模型。将圆A简化成一个质点$P_A$,那么B就要相应地变成半径为$r_{A}+r_{B}$的圆。运行的下一时刻,只要点$P_A$不出现在下图中阴影区域,圆A和圆B就不会碰撞。
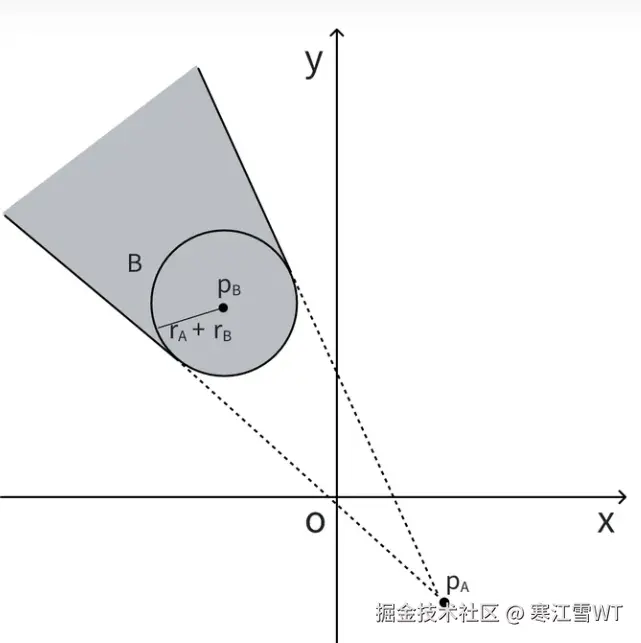
为了后续计算简便,将上面的坐标系转换为以点$P_A$为参照的坐标系,也就是将$P_A$当作坐标系原点进行计算。
计算避障的核心是控制物体的速度,因此坐标系转需要从上面的位置坐标系转换为速度坐标系。也就是说,X轴表示X方向的速度,即X方向上单位时间移动的距离,Y轴同理。因此只需要位置坐标系的所有坐标都除以单位时间τ,就可以得到速度坐标系坐标了。
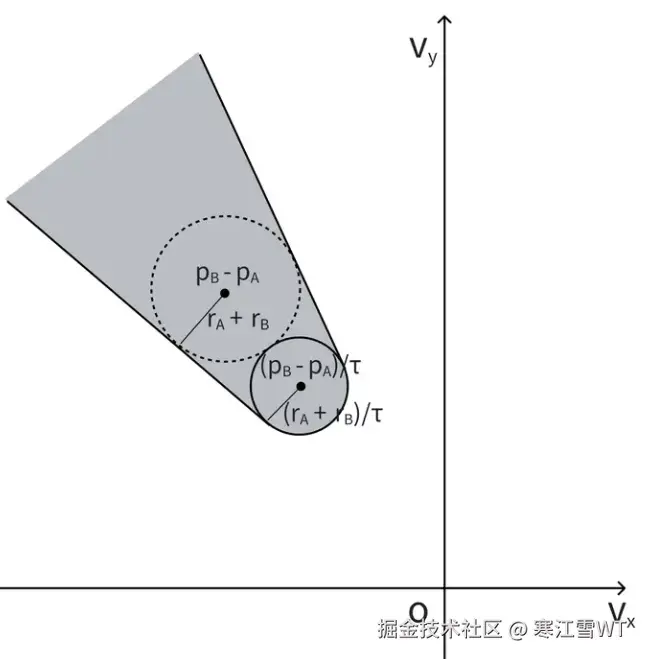
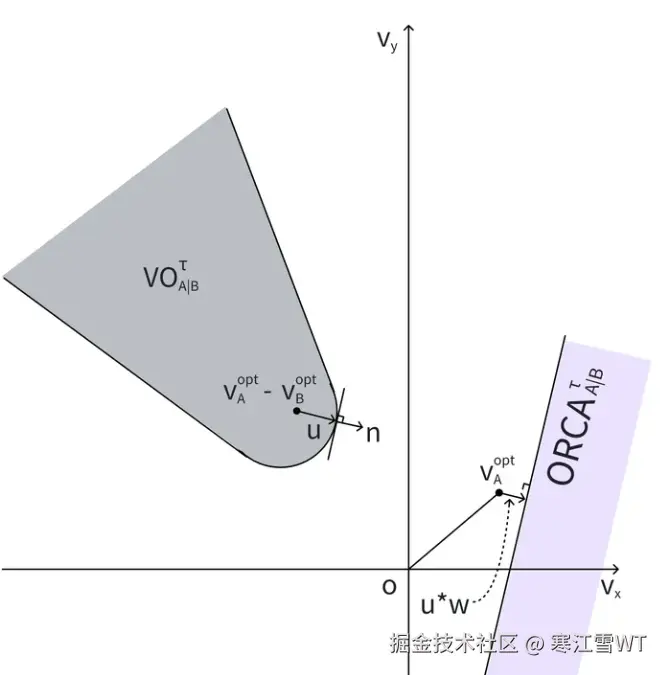
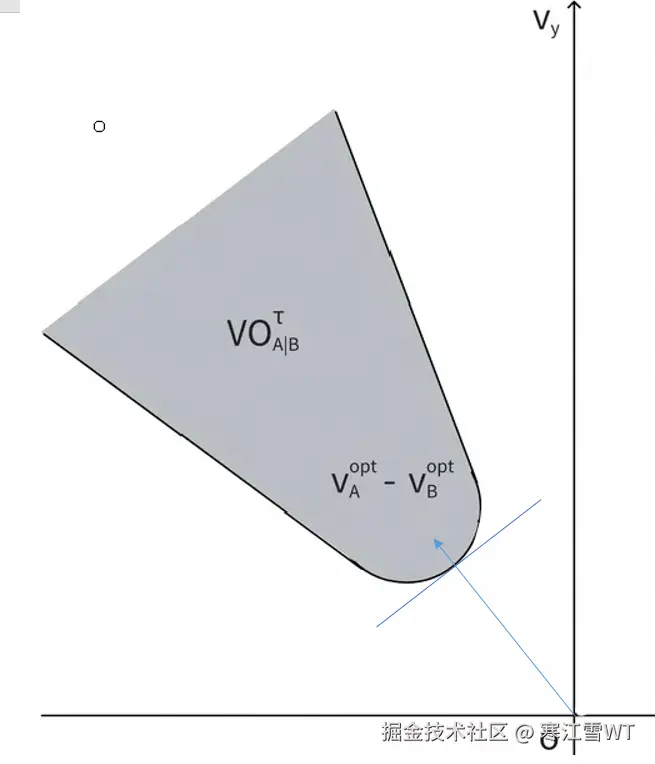
上图中,因为所有坐标都除以了τ,因此阴影区域的形状也发生了改变,原来以$P_A+P_B$为圆心、$r_A+r_B$为半径的大圆,变成了以$\frac{(P_A+P_B)}{τ}$为圆心、$\frac{(r_A+r_B)}{τ}$为半径的小圆。图中阴影区域就是速度障碍域,RVO2算法就是计算物体A和物体B的相对速度,如何能够以最小的偏移偏离这个区域。如下图所示,假设物体A和B的相对速度为$V_A^{opt}-V_B^{opt}$。则修正向量$u$如下图所示,修正量为$w$。在官方提供的实现中,$w$为0.5,然而实际应用中,不能总假设遇到的行为体都是运动的,因此有必要调整$w$的值。
基于$u$, $w$ $w$$V_A^{opt}$,计算出下图右边的半平面,它表示在A的速度可以偏移到半平面右边的位置,都可以避免碰撞。并且,有多个物体时,计算出的所有半平面相互交织,计算偏转速度,就成了一个线性规划问题。
存在的问题
然而,所提出的RVO2算法,是存在缺点的。目前发现有如下三个:
- 完全对向移动的物体无法避碰。
- $w$的权值计算。
- 速度障碍域的死锁区域。
完全对向移动的物体无法避碰
产生该问题的主要原因是当相对速度正好是速度障碍域的中心线时,每一轮迭代计算的速度都是中心线,速度方向不变,速度大小越来越小。解决该问题的方法是给期望速度增加一个随机的抖动,使双向移动的物体的速度,不可能在数值上完全平行。
$w$权值的计算
在官方提供的实现中,$w$为0.5,然而实际应用中,不能总假设遇到的行为体都是运动的,因此有必要调整$w$的值。该权值可以自定义,我测试的方法是使用速度大小来评估权值$w$,公式如下:
$w = \frac{V_{self}}{V_{self}+V_{other}}$
这样当另一个Agent速度大小为0时,$w$为1。
速度障碍域的死锁区域
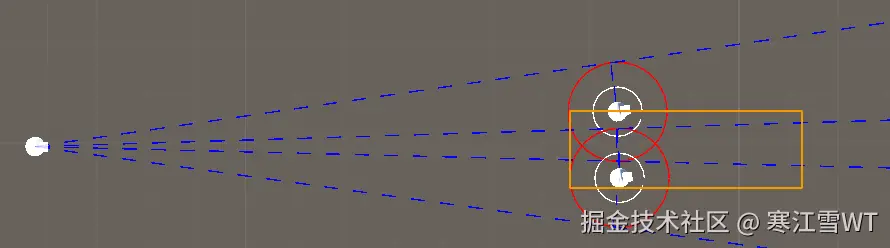
速度障碍域的死锁区域是RVO2本身的缺陷。造成该问题的根本原因是多个速度障碍的重叠。如下图,橙色框住的部分是重叠的。左边Agent的前进速度,在上下两个速度障碍域对速度的修正,最后都会落到中间重叠的位置,越靠近右边两个Agent,线性规划的结果会越来越小。下面重点分析这个问题:
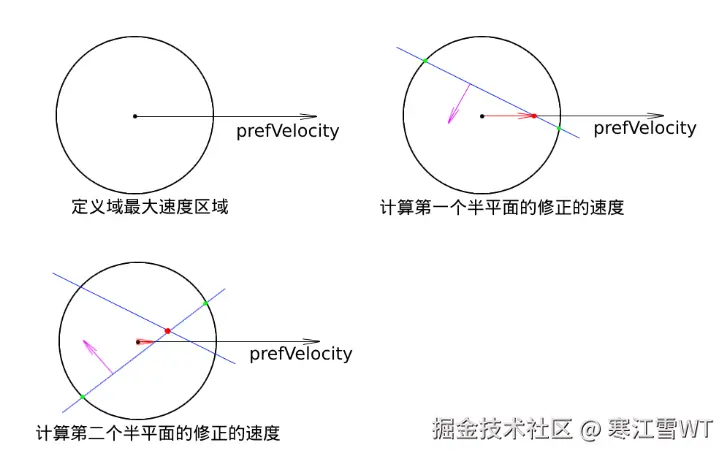
首先,第一步是以最大速度为半径画圆,表明对该Agent的修正速度,都只能落在这个圆内。
第二步,对第一个半平面进行处理,图中紫色为该直线的法线,表明在法线的区域内都是合法的速度。在这里,先计算直线与圆的交点(图中绿色的点),然后计算$PrefVelocity$与直线的交点,如果在色点范围之外,则选取绿色的点作为新的速度方向,否则取交点作为新速度的方向。
第三步,对第二个半平面进行处理。在这里,先计算直线与圆的交点(图中绿色的点),然后计算当前直线与之前处理的直线的交点,根据交点的方位,将绿色的点收缩到合法范围内。这里第一条直线已经将圆切成了两个部分,第二条直线的范围受第一条直线的影响,所以进行求交,收缩。最后计算$PrefVelocity$与第二条直线的交点,判断是否在收缩后的点的范围内,如果在可以作为新的修正速度,否则只能在边界点选择。
可以看到,第二次修正时,速度会变得非常小,这在模拟过程中可以观察得到。而圆的半径(最大速度)并不影响这个计算结果。
为了解决这个问题,在没有全局地图信息的情况下,我先后尝试了下面的方法,对于解决死锁问题是可行的,但是在进行大规模测试的时候,会出现新的问题:
- 最小速度限制
- 去掉RVO2的最小修正约束,每次都进行较大的修正。
- 根据周围的Agent定制绕行方向
- 设置偏转方向约束
- 以$PrefVelocity$为中心,向周围Agent展开,获得最大绕行方向。
- 在评估的绕行方向上计算新的途径点
上述方法中,基本都能解决重叠区域死锁的问题,但会导致循环问题,或无目的地游走等不自然的现象等。
出现这些问题的根本原因是RVO2性质导致的:
- RVO2算法本质是一个贪心策略,总是根据当前的$PrefVelocity$来进行规划,得到的是每一次迭代的局部最优解。
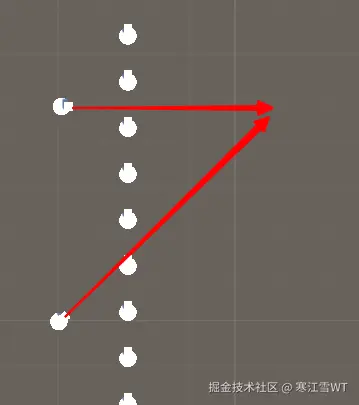
- 算法是没有全局信息和历史决策信息的,因此在信息缺失的情况下做决策,得到的结果必然不准确。比如循环问题的发生,是由于前一次决策时$PrefVelocity$被修正较大,Agent进行绕行,绕行的距离较远时,周围的Agent信息发生了改变,新的$PrefVelocity$被判断为反方向绕行,所以Agent又绕回去,形成反复。如下图所示,Agent在上面的状态时,显示向右方向不可行,向下移动,紧接着新的$PrefVelocity$表明应该向上运动,就形成反复了。这就是由于缺少全局信息导致的。
解决办法
- 让Agent之间的间隔,总是至少能容得下一个Agent通行,缺点就是Agent和Agent之间比较漏。
- 允许速度障碍域重叠,但是当有Agent要通行时,要进行避让,消除重叠区域,缺点就是要给Agent设计避让逻辑。
- 修改RVO2算法,把重叠的速度障碍域的并集当作新的速度障碍域,对速度进行修正。缺点就是修正量会比较大,还没有这方面可参考的资料。
参考资料
[1] https://zhuanlan.zhihu.com/p/669426124
[2] https://www.bilibili.com/video/BV1qa4y117Yo/?vd_source=3c157a29d0c66319c2089c40c621c2a9
[3] https://t.cj.sina.com.cn/articles/view/3743149912/df1bef5801901cp6s
