在平面中判断一个圆与矩形是否相交的方法
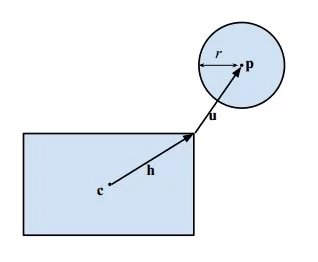
设$C$为矩形中心,$h$为矩形对角线向量的一半,$P$为圆心,$r$为半径长度
只要能计算出圆心与矩形的最短距离$u$,并与半径比较就可以判断圆与矩形是否相交
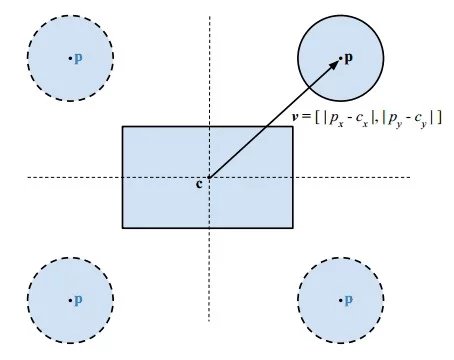
- 利用绝对值把$p-c$转移到第一象限,下图显示不同象限的圆心也能映射到第一象限,这不影响相交测试的结果。
- 然后,把v减去h,负数的分量设置为0,就得到圆心与矩形最短距离的矢量u。下图展示了四种情况,红色的u是结果。
- 然后要比较$u$和$r$的长度,若距离少于$r$,则两者相交。可以只求$u$的长度平方是否小于$r$的平方。