基于物理的渲染(PBR)
基于物理的渲染是在一种几何光学渲染模型,在于模拟真实的着色表现。在这套体系中,会有一些前提假设,比如光沿直线传播,光源辐射的能量固定,光线在物体表面会发生反射,折射的现象,物体表面会吸收光能等。辐射度理论是这套体系的基础理论,在此基础上提出微表面模型,BRDF等理论,定义了光在传播过程中如何与物体表面交互,并进入人眼的过程。
在本篇文章中,会总结辐射度理论基础,微表面模型,BRDF,最后简单介绍Metal/Roughness工作流,这是在游戏中普遍使用的一种PBR工作流。力求精确的同时,通俗解释,并联系实践。
背景
在PBR被提出之前,使用的着色模型是经典的Phong模型和进一步的Blinn-Phong模型。前者使用表面法线和光线方向直接计算表面接收到的光强度。后者更进一步,计算视线和光线求和的半程向量,并以此来计算表面接收到的光强度,这是合理的,因为只有法线为半程向量的表面反射的光才能进入人眼,但是这样又会违反物理直觉,因为物体表面的法线与半程向量可能相去甚远。不过这些理论都为后来PBR奠定了基础。
辐射度理论基础
辐射通量(Radiant Flux, $\Phi$):光源所输出的能量,以瓦特为单位。光是由多种不同波长的能量所集合而成的,而每种波长则与一种特定的(可见的)颜色相关。所以这个物理量就可以简单地理解为光源的颜色(RGB)即可。这个能量(”颜色“)从光源发出,经过物体表面,最终进入到人眼时,会减弱,而后续的理论会介绍如何计算这个衰减。
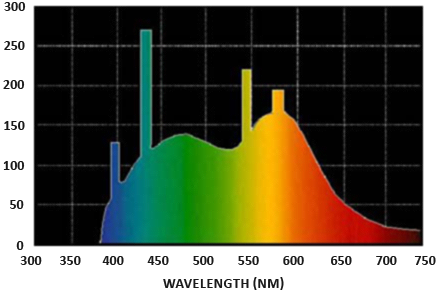
立体角(Solid Angle,$\omega$ ):单位球面上的一个截面的大小或面积,类似于二维圆上的弧度。
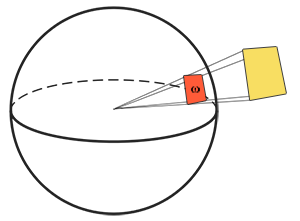
辐射强度:单位立体角上光源发射的辐射通量。$I=\frac{d\Phi}{d\omega}$
辐射率(Radiance):对单位面积,单位立体角上,辐射的总能量,用于量化来自单一方向上光线的辐射强度。它受到入射光线和平面法线间夹角余弦值的影响,当平面完全垂直于光线时辐射的能量越多。我们可以用辐射率表示单束光线穿过空间中一个点的通量。
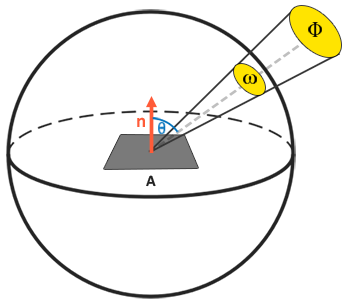
辐照度(Irradiance):表示所有投射到同一点上光线辐射率的总和。
关于上面的理论简介,已经是最简短的介绍了。用上面辐射率和辐照度的图来总结,就是以平面A为中心的单位半球平面上,一束光,携带着能量(辐射强度 $I$)照射到平面A上,这部分能量最终投影到平面A上的部分由平面法线和光线方向决定(即$n\cdot l)$,这就是辐射率(Radiance)。而来自四面八方的光线都做一遍上面的计算并求和,就是辐照度(Irradiance)。
在上面的描述中,辐射强度即光的颜色,而投影到平面A上的百分比用$n\cdot l$表示,两者相乘即为平面A接收的来自所有方向的有效能量了。
反射与散射
反射即为光线在介质交界处改变传播方向,返回原来的介质的现象。
散射即为光线在介质交界处改变传播方向,透过交界面进入新介质的现象,这些光一部分被介质吸收,一部分又被散射到外部,称为次表面散射光。
下图很好地表示了这个过程。

金属材质的物体,散射到内部的光线会被全部吸收,因此不存在散射到外部的说法。而非金属物体会吸收一部分频率的光线,光强会因为吸收而减小。透明介质因为无折射率变化,不存在散射,只发生折射,光在折射后继续沿直线传播,不会再反弹回原介质。
结合上面的基础理论。为了保持思路清晰,到这里再做一个小结。即平面A收到一束光源照射的能量之后,将一部分能量反射出去,一部分能量被吸收,由重新散射出去。而这就需要计算有多少能量反射出去,有多少能量被散射出去了。这就引出了后面要介绍的微平面模型,这里所说的平面A其实就是一个微平面,后面再介绍。
微平面模型
微平面理论(Microfacet Theory)认为达到微观尺度后,平面可以视作很多绝对光滑的镜面组成。大的平面越是粗糙,微平面的排列越混乱,导致入射光线反射方向越是杂乱,以至于完全发散开来。也就是说越粗糙的表面的镜面反射范围更广,越光滑的表面光线反射方向越接近,范围乐锐利,如下图所示,引自《Moving Frostbite to PBR,SIGGRAPH 2014》。
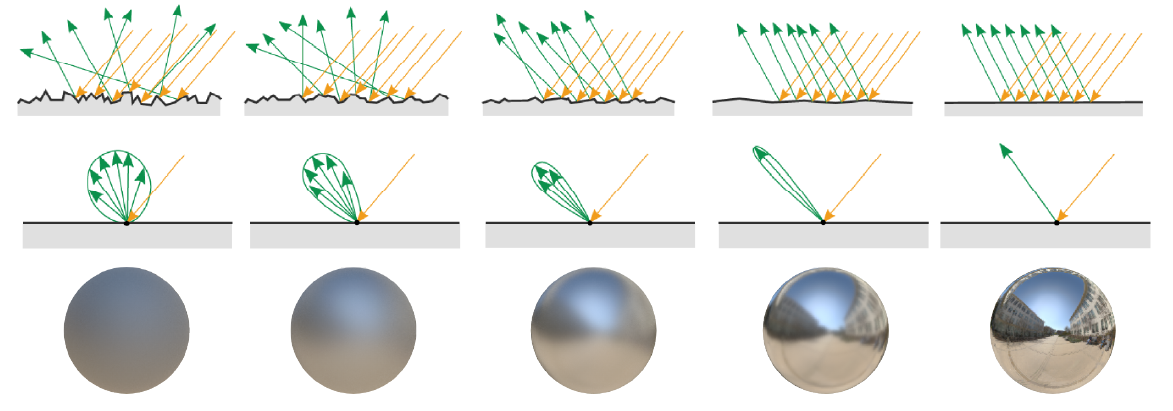
这里提到的微平面就是PBR体系中的基础假设,但是对于初学者来说,难免难以理解微平面在程序里如何表示。其实不用表示,在光栅渲染器中是一个片元,在光线追踪里是光线与物体表面相交的一个点。而在此基础上,就衍生出后来的BRDF理论,用来计算前面提到的,反射光线的百分比,散射光线的百分比。
我对于微平面的理解,即一个着色表面之下,可以分成许数个微小的光滑镜面,这个着色表面被光照射时所呈现出来的效果,就是由这些微小的光滑镜面与光交互时,光发生反射现象,如果这些微小的镜面的朝向并不总是与着色表面一致,因此表现出表面粗糙的现象,而较平滑的表面,则微小的光滑镜面朝向较一致,反射光线也较为一致,表现出镜面的效果。这一段理解之后,BRDF在做的事情,就不难理解了,即评估有多少反射光线会进入人眼,即平面A收到来自各方向光的能量,最终进入人眼的能量所占的百分比。
渲染方程
在介绍BRDF之前,首先介绍渲染方程。
其中$L_o$为$p$点的出射辐射率,$f_r$是$p$点入射方向到出射方向光的反射比,也叫双向反射分布函数(BRDF),$L_i$是$p$点入射光辐射率。渲染方程说明了$p$点的出射辐射率,可以通过半球$\Omega$内所有入射方向光线辐射率乘以$f_r$,和余弦值$n \cdot \omega_i$ 。
还是用上面的平面A来解释,$L_i(p,\omega_i)n\cdot\omega_i$即一束光照射到平面A上的能量,$f_r(p,\omega_i,\omega_o)$即评估反射到人眼中光线的比例。积分则表示所有光线的方向。由此即可得到从某个方向观察一个着色点时,进入眼睛的能量大小。
双向反射分布函数(BRDF)
双向反射分布函数接受入射光方向$\omega_i$,出射(观察)方向$\omega_o$,平面法线$n$以及一个用来表示位于点$p$的微平面的粗糙度系数$\alpha$。对于一个给定了材质属性的微平面,BRDF可以近似地计算出每束光线在该微平面上最终反射出来的光线能量的占比,这和观察方向$\omega_o$是紧密相关的。譬如说,一个完美的镜面,BRDF函数只在一个观察方向上返回1.0,而其他反向都是0,因为只有一个方向能接收到反射光线,且不会有散射光线。
对于一个BRDF,为了实现物理学上的可信度,它必须遵守能量守恒定律,也就是说反射光线的总和永远不能超过入射光线的总量。严格上来说,同样采用$\omega_i$和$\omega_o$作为输入参数的 Blinn-Phong光照模型也被认为是一个BRDF。然而由于Blinn-Phong模型并没有遵循能量守恒定律,因此它不被认为是基于物理的渲染。现在已经有很好几种BRDF都能近似的得出物体表面对于光的反应,但是几乎所有实时渲染管线使用的都是一种被称为Cook-Torrance BRDF模型。
Cook-Toorance模型
Cook-Torrance BRDF兼有漫反射和镜面反射两个部分:
这里$k_d$是被折射部分能量所占的比例,而在实现中,会根据材质参数进一步计算出散射部分所占的比例,这个意识很重要,因为不是所有折射进表面内部的光线都会被散射出来,比如金属材质。$k_s$是被反射的部分比例。不过后续再介绍$f_{cook-torrance}$时,$k_s$会合并到公式里去,这在下文中会介绍。
$f_{cook-torrance}$的形式如下:
Cook-Torrance BRDF的镜面反射部分包含三个函数,此外分母部分还有一个标准化因子 。字母D,F与G分别代表着一种类型的函数,各个函数分别用来近似的计算出表面反射特性的一个特定部分。三个函数分别为法线分布函数(Normal Distribution Function),菲涅尔方程(Fresnel Rquation)和几何函数(Geometry Function):
法线分布函数:估算在受到表面粗糙度的影响下,朝向方向与半程向量一致的微平面的数量。这是用来估算微平面的主要函数。
几何函数:描述了微平面自成阴影的属性。当一个平面相对比较粗糙的时候,平面表面上的微平面有可能挡住其他的微平面从而减少表面所反射的光线。
菲涅尔方程:菲涅尔方程描述的是在不同的表面角下表面所反射的光线所占的比率。而这就是前面提到的$k_s$,所以说$k_s$是被合并到了公式中
以上的每一种函数都是用来估算相应的物理参数的,而且你会发现用来实现相应物理机制的每种函数都有不止一种形式。它们有的非常真实,有的则性能高效。你可以按照自己的需求任意选择自己想要的函数的实现方法。Epic游戏公司的Brian Karis对于这些函数的多种近似实现方式进行了大量的研究。在UE4中,D使用Trowbridge-Reitz GGX,F使用Fresnel-Schlick近似(Fresnel-Schlick Approximation),而G使用Smith’s Schlick-GGX。
法线分布函数
法线分布函数D,从统计学上近似地表示了与某些(半程)向量$h$取向一致的微平面的比率。举例来说,假设给定向量$h$,如果我们的微平面中有35%与向量$h$取向一致,则法线分布函数或者说NDF将会返回0.35。目前有很多种NDF都可以从统计学上来估算微平面的总体取向度,只要给定一些粗糙度的参数。
由此可见,法线分布函数是用来估计一个微平面下的完美镜面微小平面的法向量与半程向量$h$一致的微小平面数量占总数的百分比,是一个估值,这是理解法线分布函数的关键。而之所以取半程向量,是因为只有法线方向为半程向量的平面的反射光线能与$\omega_o$一致。
下面是Trowbridge-Reitz GGX的实现公式:
几何函数
几何函数从统计学上近似的求得了微平面间相互遮蔽的比率,这种相互遮蔽会损耗光线的能量。几何函数也是要给估值,即是说一个微平面下的完美微小镜面平面相互之间会发生遮挡,进而阻挡反射光线进入人眼,因此几何函数就是用来估算遮挡程度作为能量的损耗。

下面是Schlick-GGX的实现:
其中,$k$是由象征粗糙度的$\alpha$计算而来,而$k$的计算取决于我们要用的是针对直接光照还是针对IBL光照的几何函数:
为了有效的估算几何部分,需要将观察方向(几何遮蔽(Geometry Obstruction))和光线方向向量(几何阴影(Geometry Shadowing))都考虑进去。可以使用史密斯法(Smith’s method)来把两者都纳入其中:
上面这个公式同时考虑了观察方向的遮蔽以及入射光方向的遮蔽,这是合理的,因为观察方向的遮蔽会导致反射光线的收阻,而入射光方向的遮蔽会导致平面无法接收到光线,就无法产生反射光线。
菲涅尔方程
菲涅尔方程描述的是被反射的光线对比光线被折射的部分所占的比率,这个比率会随着我们观察的角度不同而不同。当光线碰撞到一个表面的时候,菲涅尔方程会根据观察角度告诉我们被反射的光线所占的百分比。利用这个反射比率和能量守恒原则,可以直接得出光线被折射的部分以及光线剩余的能量。
当垂直观察的时候,任何物体或者材质表面都有一个基础反射率(Base Reflectivity),但是如果以一定的角度往平面上看的时候所有反光都会变得明显起来。
菲涅尔方程是一个相当复杂的方程式,不过幸运的是菲涅尔方程可以用Fresnel-Schlick近似法求得近似解:
然后正如你可以从球体表面看到的那样,我们越是朝球面掠角的方向上看(此时视线和表面法线的夹角接近90度)菲涅尔现象就越明显,反光就越强:

菲涅尔方程计算的就是$k_s$,$k_d$是由$k_s$计算而来,公式是:
漫反射部分
回到Cook-Toorance模型,$k_df_{lambert}$是Cook-Toorance模型的漫反射部分,也叫散射部分。由上可知,$k_d = 1 - k_s$,是光线折射进入物体后,未被物体吸收重新进入空气中的部分。而这里,还要定义一个被吸收的比例才完整,这个比例就是金属度(Metallic)。纯金属的表面,在光线折射进入物体后,会被完全吸收,所以不会有散射的光线,而非金属材质,会将光线完全散射进入空气中,而这部分散射光线的比例,就由金属度控制。漫反射部分的完整公式如下:
这里$\beta$即为金属度,是一个0到1的值。
$f_{lambert}$表示漫反射能量:
除以$\pi$是为了对漫反射光进行标准化,因为前面含有BRDF的渲染方程是受$\pi$影响的。
Metallic/Roughness工作流
金属度/粗糙度工作流指的是将上述参数都用纹理进行表示,结合法线/视差纹理,AO贴图一起来表示材质的表面属性。而美术人员只需要根据需要创作上面的纹理即可得到符合物理的渲染效果。
不过需要注意的是一般来说反射率(albedo)纹理在美术人员创建的时候就已经在sRGB空间了,因此我们需要在光照计算之前先把他们转换到线性空间。一般来说,环境光遮蔽贴图(ambient occlusion maps)也需要我们转换到线性空间。不过金属性(Metallic)和粗糙度(Roughness)贴图大多数时间都会保证在线性空间中。
除了金属度/粗糙度工作流只外,还有镜面反射/光泽度工作流(M/R),这里就不介绍了。
