海面模拟（一）

Ray Tracing The Rest of Your Life

  作者：Peter Shirley, Trevor David Black, Steve Hollasch

1. 概述

  在《Ray Tracing in One Weekend》和《Ray Tracing: the Next Week》，你构建了一个”真正的“光线跟踪渲染器。

  如果你学有余力，你可以利用这些书中包含的来源和信息来实现你想要的任何视觉效果。这些代码提供了一个有意义且强大的基础，在此基础上可以构建基于追踪的小型项目。商业光线追踪渲染器中的大多数视觉效果都依赖的技术在前两本书中都有描述。但是，由于缺少数学基础，您添加越来越复杂的视觉效果（如次表面散射或嵌套电介质）的能力将受到严重限制。在本书中，我假设您是一位非常感兴趣的学生，或者是正在从事与光线跟踪相关职业的人。我们将深入研究一个严谨的光线追踪渲染器中所依赖的数学原理。完成后，你应该能够很好地使用和修改许多常用领域（如电影、电视、产品设计和建筑行业）中用到的各种商用光线追踪渲染器。

  在这本短短的书中，我没有提及特别多的事情。例如，编写Monte Carlo渲染程序的方法有很多种，我只深入研究其中一种。我不介绍阴影射线（而是改用让光线更有可能射向光源的方案），也不介绍双向方法（Bidirectional Methods）、随机采样方法（Metropolis）或光子映射方法（Photon Mapping）。你会在很多所谓的“严谨光线追踪渲染器”中找到这些技术，但此处不介绍它们，因为介绍这些领域的概念、数学和术语更为重要。我认为这本书是一次深入的接触，应该是你第一次接触，它将为你提供学习这些和其他有趣技术所需的一些概念、数学和术语。

  我希望你和我一样觉得数学很吸引人。

  可以从Github仓库的README文件中找到关于本工程的信息，了解目录结构，编译和运行方法以及引用，更正和为该项目做贡献的方法描述。

  与此之前，查看我们扩展阅读的wiki页面以获取其他关于本工程的信息。

  这些书籍已经排版完毕，可以直接在你的浏览器中正确显示。我们还在“Assets”分区中包含每本书的PDF。

  感谢所有为这个项目做出贡献的人。你可以在本书末尾的致谢部分找到它们。

2. 简单的蒙特卡洛程序

  让我们从一个简单的蒙特卡洛程序开始。如果你不熟悉蒙特卡洛程序，那么最好停下来先看一看这部分的内容。有两种随机算法：蒙特卡洛算法（Monte Carlo） 和拉斯维加斯算法（Las Vegas）。随机算法在计算机图形学中随处可见，因此获得一个适当的基础并不是一个坏主意。随机算法在计算中使用了一定量的随机性。拉斯维加斯随机算法总是产生正确的结果，而蒙特卡洛算法只是可能产生正确的结果——而且经常出错！但对于光线追踪等特别复杂的问题，我们可能不会像在合理的时间内获得答案那样重视完全的准确性。拉斯维加斯算法最终会得出正确的结果，但我们可能会耗费非常多的时间。拉斯维加斯算法的经典示例是 快速排序算法。快速排序算法将始终以完全排序的列表为正确的输出形式，但是算法所需的时间是随机的。拉斯维加斯算法的另一个很好的例子是我们用来在单位球体中选择一个随机点的代码：

inline vec3 random_in_unit_sphere() {
    while (true) {
        auto p = vec3::random(-1,1);
        if (p.length_squared() < 1)
            return p;
    }
}

  这一段代码最终总是会到达单位球体中的随机点，但我们不能事先知道需要多长时间。它可能只需要1次迭代，也可能需要2,3,4甚至更多次迭代。然而，蒙特卡洛算法将给出答案的统计估计，并且你运行的时间越长，该估计会变得越来越准确。这意味着在某个时刻，我们可以判断计算的答案误差已经很小，然后退出程序。蒙特卡洛算法的基本特征就是有噪声但却能获得更接近正确结果的答案。特别适用于不需要特别高精度的图形算法等应用程序。

2.1. 估计$\pi$

  蒙特卡洛算法的经典例子就是估计 $\pi$的值，我们可以先尝试实现这个程序。有很多方法可以估计 $\pi$，其中蒲丰投针问题（Buffon’s nedle problem）是一个经典的研究案例。在蒲丰投针问题中，人们看到一个由平行地板条组成的地板，每个地板条的宽度相同。如果一根针随机掉在地板上，那么针横跨两块板的概率是多少？（你可以在网上搜索关于这个问题的相关信息）

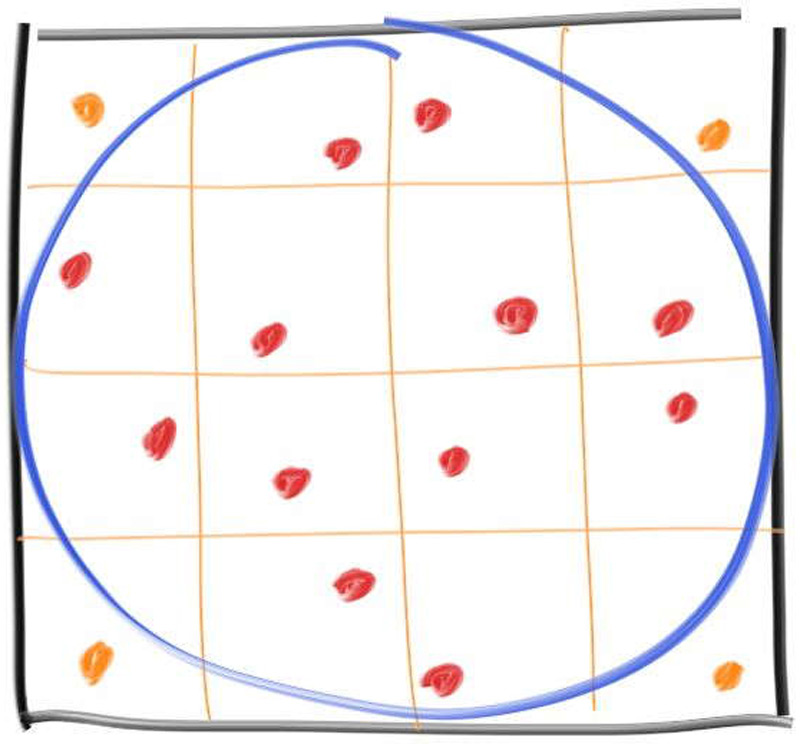
  我们将做一个受这种方法启发的变体。假设有一个圆内切在一个正方形内：

  现在，假设在正方形内选择一个随机点。最终位于圆内的那些随机点的比例应与圆的面积成正比。该比例实际上应该是圆面积与正方形面积的比：

$$\frac{\pi r^2}{(2r)^2} = \frac{\pi}{4}$$

  由于$r$被抵消了，所以$r$可以是任意值。让我们用$r=1$来做，以原点为中心：

#include "rtweekend.h"

#include <iostream>
#include <iomanip>

int main() {
    std::cout << std::fixed << std::setprecision(12);

    int inside_circle = 0;
    int N = 100000;

    for (int i = 0; i < N; i++) {
        auto x = random_double(-1,1);
        auto y = random_double(-1,1);
        if (x*x + y*y < 1)
            inside_circle++;
    }

    std::cout << "Estimate of Pi = " << (4.0 * inside_circle) / N << '\n';
}

  由于不同机器使用的初始随机数种子不同，$\pi$的估算结果可能会有差异。在我的机器上，$\pi$的估算结果是3.143760000000。

2.2. 收敛趋势

  如果我们让程序一直无限循环下去，并且打印每一次估计的结果，会发现随着迭代次数的增多，估计结果是收敛的：

#include "rtweekend.h"

#include <iostream>
#include <iomanip>

int main() {
    std::cout << std::fixed << std::setprecision(12);

    int inside_circle = 0;
    int runs = 0;
    while (true) {
        runs++;
        auto x = random_double(-1,1);
        auto y = random_double(-1,1);
        if (x*x + y*y < 1)
            inside_circle++;

        if (runs % 100000 == 0)
            std::cout << "\rEstimate of Pi = " << (4.0 * inside_circle) / runs;
    }

    // std::cout << "Estimate of Pi = " << (4.0 * inside_circle) / N << '\n';
}

2.3. 分层抽样

  我们很快就会接近 （$pi$），然后误差会越来越小。这是收益递减法则的一个例子，即每个样本的收益都比上一个小。这是蒙特卡洛最糟糕的地方。我们可以通过对样本进行分层（通常也称为抖动）来减轻这种递减的影响，方法是我们不再随机采样，而是取一个网格并在每个网格中抽取样本：

  这会改变样本的生成结果，但我们需要提前知道我们要采集多少样本。让我们以100万个样本为例，并比较两种抽样方式的结果：

#include "rtweekend.h"

#include <iostream>
#include <iomanip>

int main() {
    std::cout << std::fixed << std::setprecision(12);

    int inside_circle = 0;
    int inside_circle_stratified = 0;
    int sqrt_N = 1000;

    for (int i = 0; i < sqrt_N; i++) {
        for (int j = 0; j < sqrt_N; j++) {
            auto x = random_double(-1,1);
            auto y = random_double(-1,1);
            if (x*x + y*y < 1)
                inside_circle++;

            x = 2*((i + random_double()) / sqrt_N) - 1;
            y = 2*((j + random_double()) / sqrt_N) - 1;
            if (x*x + y*y < 1)
                inside_circle_stratified++;
        }
    }

    std::cout
        << "Regular    Estimate of Pi = "
        << (4.0 * inside_circle) / (sqrt_N*sqrt_N) << '\n'
        << "Stratified Estimate of Pi = "
        << (4.0 * inside_circle_stratified) / (sqrt_N*sqrt_N) << '\n';
}

  在我的机器上，结果如下：

Regular    Estimate of Pi = 3.141184000000
Stratified Estimate of Pi = 3.141460000000

  $\pi$的12位小数如下：

3.141592653589

  可以看到，分层抽样方法不仅更好，而且收敛的渐进更好。不幸的是，这种优势会随着问题的维度增加而减小（例如，对于3D球体体积，间隙会更小）。光线跟踪算法是一个高维度的算法，每一次反射会增加两个维度：$\phi_o$和$\theta_o$。在本书中，我们不会对输出射线的反射角度进行分层，因为它有点太复杂了，无法进行，但目前在这个领域也有很多有趣的研究。

  作为替代，我们将围绕每个像素的位置对采样点的位置进行分层。让我们从我们熟悉的康奈尔盒子场景开始。

#include "rtweekend.h"

#include "camera.h"
#include "hittable_list.h"
#include "material.h"
#include "quad.h"
#include "sphere.h"

int main() {
    hittable_list world;

    auto red   = make_shared<lambertian>(color(.65, .05, .05));
    auto white = make_shared<lambertian>(color(.73, .73, .73));
    auto green = make_shared<lambertian>(color(.12, .45, .15));
    auto light = make_shared<diffuse_light>(color(15, 15, 15));

    // Cornell box sides
    world.add(make_shared<quad>(point3(555,0,0), vec3(0,0,555), vec3(0,555,0), green));
    world.add(make_shared<quad>(point3(0,0,555), vec3(0,0,-555), vec3(0,555,0), red));
    world.add(make_shared<quad>(point3(0,555,0), vec3(555,0,0), vec3(0,0,555), white));
    world.add(make_shared<quad>(point3(0,0,555), vec3(555,0,0), vec3(0,0,-555), white));
    world.add(make_shared<quad>(point3(555,0,555), vec3(-555,0,0), vec3(0,555,0), white));

    // Light
    world.add(make_shared<quad>(point3(213,554,227), vec3(130,0,0), vec3(0,0,105), light));

    // Box 1
    shared_ptr<hittable> box1 = box(point3(0,0,0), point3(165,330,165), white);
    box1 = make_shared<rotate_y>(box1, 15);
    box1 = make_shared<translate>(box1, vec3(265,0,295));
    world.add(box1);

    // Box 2
    shared_ptr<hittable> box2 = box(point3(0,0,0), point3(165,165,165), white);
    box2 = make_shared<rotate_y>(box2, -18);
    box2 = make_shared<translate>(box2, vec3(130,0,65));
    world.add(box2);

    camera cam;

    cam.aspect_ratio      = 1.0;
    cam.image_width       = 600;
    cam.samples_per_pixel = 64;
    cam.max_depth         = 50;
    cam.background        = color(0,0,0);

    cam.vfov     = 40;
    cam.lookfrom = point3(278, 278, -800);
    cam.lookat   = point3(278, 278, 0);
    cam.vup      = vec3(0, 1, 0);

    cam.defocus_angle = 0;

    cam.render(world);
}

  运行上面的程序，生成一张非分层抽样渲染的图并保存，用于比较。

  现在，做如下修改，实现分层抽样方法：

class camera {
  public:
    ...

    void render(const hittable& world) {
        initialize();

        std::cout << "P3\n" << image_width << ' ' << image_height << "\n255\n";

        for (int j = 0; j < image_height; j++) {
            std::clog << "\rScanlines remaining: " << (image_height - j) << ' ' << std::flush;
            for (int i = 0; i < image_width; i++) {
                color pixel_color(0,0,0);
                for (int s_j = 0; s_j < sqrt_spp; s_j++) {
                    for (int s_i = 0; s_i < sqrt_spp; s_i++) {
                        ray r = get_ray(i, j, s_i, s_j);
                        pixel_color += ray_color(r, max_depth, world);
                    }
                }
                write_color(std::cout, pixel_samples_scale * pixel_color);
            }
        }

        std::clog << "\rDone.                 \n";
    }

  private:
    int    image_height;         // Rendered image height
    double pixel_samples_scale;  // Color scale factor for a sum of pixel samples
    int    sqrt_spp;             // Square root of number of samples per pixel
    double recip_sqrt_spp;       // 1 / sqrt_spp
    point3 center;               // Camera center
    ...

    void initialize() {
        image_height = int(image_width / aspect_ratio);
        image_height = (image_height < 1) ? 1 : image_height;

        sqrt_spp = int(std::sqrt(samples_per_pixel));
        pixel_samples_scale = 1.0 / (sqrt_spp * sqrt_spp);
        recip_sqrt_spp = 1.0 / sqrt_spp;

        center = lookfrom;
        ...
    }

    ray get_ray(int i, int j, int s_i, int s_j) const {
        // Construct a camera ray originating from the defocus disk and directed at a randomly
        // sampled point around the pixel location i, j for stratified sample square s_i, s_j.

        auto offset = sample_square_stratified(s_i, s_j);
        auto pixel_sample = pixel00_loc
                          + ((i + offset.x()) * pixel_delta_u)
                          + ((j + offset.y()) * pixel_delta_v);

        auto ray_origin = (defocus_angle <= 0) ? center : defocus_disk_sample();
        auto ray_direction = pixel_sample - ray_origin;
        auto ray_time = random_double();

        return ray(ray_origin, ray_direction, ray_time);
    }

    vec3 sample_square_stratified(int s_i, int s_j) const {
        // Returns the vector to a random point in the square sub-pixel specified by grid
        // indices s_i and s_j, for an idealized unit square pixel [-.5,-.5] to [+.5,+.5].

        auto px = ((s_i + random_double()) * recip_sqrt_spp) - 0.5;
        auto py = ((s_j + random_double()) * recip_sqrt_spp) - 0.5;

        return vec3(px, py, 0);
    }

    vec3 sample_square() const {
        ...
    }

    ...
};

  下图是没有使用分层抽样的结果：

  下图是使用了分层抽样的结果：

  如果你眯着眼睛，应该能够在平面边缘和框的边缘看到更清晰的对比度。这种效果在变化频率较高的位置会更加明显。高频变化也可以被认为是高信息密度。对于我们的Cornell box场景，我们所有的材质都是表面粗糙的，头顶上有柔和的区域光，因此唯一信息密度高的位置是在对象的边缘。纹理和反光材质的效果会更加明显。

  如果你曾经做过单反射或阴影或一些严格的2D问题，你肯定想要对问题进行分层。

3. 一维蒙特卡罗积分

  前面提到的蒲丰投针问题是一种通过计算圆面积与方形面积的比例来计算$\pi$的方式：

$$\frac{area(circle)}{area(square)}=\frac{\pi}{4}$$

  我们在方形区域内随机选择大量的点，并统计那些在单位圆内的点。随着随机采样点的增加，估计值收敛于$\frac{\pi}{4}$。即便我们不知道圆的面积，仍然可以求解上上述比值。我们知道计算圆面积与外接正方形面积的比值为$\frac{\pi}{4}$，并且我们知道圆外接正方形的面积计算公式为$4r^2$ ，因此，我们可以使用这两个公式，来推出圆的面积公式：

$$\frac{area(circle)}{area(square)}=\frac{\pi}{4}\\ \frac{area(circle)}{(2r)^2}=\frac{\pi}{4}\\ area(circle)=\frac{\pi}{4}4r^2\\ area(circle)=\pi r^2$$

  我们可以让圆的半径$r=1$，然后得到：

$$area(circle)=\pi$$

  我们上面求解$\pi$的方法和求解圆面积的方法是等效的。因此，我们可以在求解$\pi$的程序的第一个版本中进行以下替换：

//	std::cout << "Estimate of Pi = " << (4.0 * inside_circle) / N << '\n';
std::cout << "Estimated area of unit circle = " << (4.0 * inside_circle) / N << '\n';

3.1. 期望值

  让我们退一步来看看蒙特卡洛算法是否更具有普遍性。

  如果我们假设有以下条件：

1. 集合$X$，包含$x_i$。

$$X = (x_0,x_1,x_2,x_3....,X_{N-1})$$

1. 一个连续函数$f(x)$，以$x_i$为自变量：

$$y_i = f(x_i)$$

1. 一个函数$F(X)$以集合$X$种的元素来输入，输出集合$Y$：

$$Y = F(X)$$

1. 输出的$Y$集合，及其元素构成如下：

$$Y=(y_0,y_1,y_2,....,y_{N-1}) = (f(x_0),f(x_1),f(x_2),.....,f(x_{N-1})$$

  基于上述假设前提，我们可以用下面的方法计算集合$Y$的算数平均值：

$$\begin{align} average(Y_i) &= E[Y]=\frac{1}{N}\sum_{i=0}^{N-1}y_i\\ &=\frac{1}{N}\sum_{i=0}^{N-1}f(x_i)\\ &=E[F(X)] \end{align}$$

  其中，$E[Y]$是$Y$的期望值。

  注意，这里平均值和期望值之间的细微差别：

• 一个集合可能包含来自该集合的多个不同选择组成的子集。每个子集都有一个平均值，即所有选择的总和除以选择的数量。请注意，父集合中的元素可能在子集中出现零次、一次或多次。
• 一个集合只有一个期望值，计算方法为：该集合的所有元素的总和，除以元素的总数量。换句话说，期望值就是一个集合中所有元素的平均值。

  需要理解一个重要的概念，当随着随机样本的数量增加，采样集合的平均值会收敛于期望值。

  如果$x_i$从一个连续的区间$[a,b]$中抽取，即对于所有的$i$，$a \leq x_i \leq b$，则在区间$(a\leq x’ \leq b)$内，$E[F(X)]$约等于连续函数$f(x’)$的平均值。

$$\begin{align} E[f(x')|a\leq x' \leq b] &\approx E[F(X)|X=\{x_i|a\leq x_i \leq b\}]\\ &\approx E[Y = \{y_i = f(x_i) | a \leq x_i \leq b \}]\\ &\approx \frac{1}{N}\sum_{i=0}^{N-1}f(x_i) \end{align}$$

  如果我们让$N$趋近于$\infin$，那么可以得到下面的等式：

$$E[f(x')|a\leq x' \leq b] = \lim_{x → \infin} \frac{1}{N}\sum_{i=0}^{N-1}f(x_i)$$

  在连续区间$[a,b]$内，连续函数$f(x′)$的期望值可以通过对区间内无限数量的随机采样点求和来表示。当采样点的个数接近$\infin$时，输出的平均值趋向于精确答案。这就是蒙特卡洛算法。

  随机采样点并不是我们求解区间内期望值的唯一方法。我们还可以选择放置采样点的位置。如果我们在区间$[a,b]$上有$N$个样本，那么我们可以选择在整个区间内均匀分布点：

$$x_i = a + i\Delta x \quad i=0,1,2...N-1\\ \Delta x = \frac{b-a}{N}$$

  求解它们的期望值：

$$E[f(x')|a\leq x' \leq b]\approx \frac{1}{N}\sum_{i=0}^{N-1}f(x_i)|_{x_i=a+i\Delta x}\\ E[f(x')|a\leq x' \leq b]\approx \frac{\Delta x}{b-a}\sum_{i=0}^{N-1}f(x_i)|_{x_i=a+i\Delta x}\\ E[f(x')|a\leq x' \leq b]\approx \frac{1}{b-a}\sum_{i=0}^{N-1}f(x_i) \Delta x|_{x_i=a+i\Delta x}$$

  让$N$趋近于$\infin$：

$$E[f(x')|a\leq x' \leq b] = \lim_{N→\infin}\frac{1}{b-a}\sum_{i=0}^{N-1}f(x_i)\Delta x|_{x_i=a+i\Delta x}$$

  得到一个规则的积分式：

$$E[f(x')|a\leq x' \leq b] = \frac{1}{b-a}\int_a^bf(x)dx$$

  如果你还记得高等数学上讲过的内容，那么函数的积分就是该区间内曲线下的面积：

$$area(f(x),a,b)=\int_a^bf(x)dx$$

  因此，一个函数在区间内的期望与该区间内曲线下的面积有着内在联系：

$$E[f(x)|a\leq x \leq b]=\frac{1}{b-a}\cdot area(f(x),a,b)$$

  

  函数的积分和该函数的蒙特卡罗采样均可用于求解特定区间的平均值。积分通过区间中无数个无穷小片段的总和来求解平均值，而蒙特卡洛算法将通过求解区间内不断增加的随机样本点的总和来近似计算相同的平均值。计算物体内部的点数并不是测量其平均值或面积的唯一方法，积分也是常用的数学工具。如果问题存在封闭的，积分通常是最自然、最干净的表述方式。

  我想举几个例子会有所帮助。

3.2. $x^2$的积分

  让我们看下面的式子：

$$I=\int_0^2x^2dx$$

  我们可以用积分来解决这个问题：

$$I = \frac{1}{3}x^2|_{0}^{2}\\ I = \frac{1}{3}(2^3 - 0^3)\\ I = \frac{8}{3}$$

  或者，我们可以使用蒙特卡洛方法求解积分。在计算机科学领域中，我们可以将其写为：

$$I = area(x^2,0,2)$$

  我们还可以把它写成如下形式：

$$E[f(x)|a\leq x \leq b] = \frac{1}{b-a} \cdot area(f(x),a,b)\\ average(x^2,0,2) = \frac{1}{2-0}\cdot area(f(x),a,b)\\ average(x^2, 0, 2) = \frac{1}{2-0}\cdot I\\ I = 2 \cdot average(x^2, 0, 2)$$

  使用蒙特卡洛方法：

#include "rtweekend.h"

#include <iostream>
#include <iomanip>

int main() {
    int a = 0;
    int b = 2;
    int N = 1000000;
    auto sum = 0.0;

    for (int i = 0; i < N; i++) {
        auto x = random_double(a, b);
        sum += x*x;
    }

    std::cout << std::fixed << std::setprecision(12);
    std::cout << "I = " << (b - a) * (sum / N) << '\n';
}

  结果符合预期：输出结果几乎等于积分运算的结果。$I = 2.6666…. = \frac{8}{3}$。这个例子可以一定程度上说明了积分运算实际上比蒙特卡洛的工作量少得多。然而，该结论只对简单的函数有效（例如$f(x) = x^2$），当函数变得复杂时（例如$f(x) = sin^5(x)$），蒙特卡洛方法比积分运算要简单得多。

for (int i = 0; i < N; i++) {
    auto x = random_double(a, b);
    sum += std::pow(std::sin(x), 5.0);
}

  我们还可以使用蒙特卡洛算法来处理不存在解析积分的函数，例如$f(x) = \ln(sin(x))$：

for (int i = 0; i < N; i++) {
    auto x = random_double(a, b);
    sum += std::log(std::sin(x));
}

  在图形学中，我们经常会遇到一些可以明确写下来但需要复杂解析积分的函数，或者，我们经常遇到一些可以求值但无法明确写下来的函数，而且我们经常会发现这些函数只能通过概率求值。前两本书中的ray_color函数就是一个只能通过概率确定的函数的例子。我们无法知道从任何给定位置向所有方向可以看到什么颜色，但我们可以从统计上估计从某个特定位置向某个特定方向可以看到哪种颜色。

  译者注：ray_color函数输出的就是整个图像，输入是观察位置，观察方向等相机参数以及场景的几何结构。我们实现的ray_color实际上在做的事情就是在方向上进行采样。

3.3. 密度函数

  前两本书中，我们实现的ray_color函数，虽然简单而优雅，但却存在相当大的严重的问题。小光源产生的噪音太大。这是因为我们的均匀采样对这些光源的采样频率不够。仅当光线散射到光源时才会对光源进行采样，但对于小光源或远处的光源来说，这种情况不太可能发生。如果背景颜色是黑色，那么场景中唯一真正的光源就是实际放置在场景周围的灯光。表面上可能有两条光线在邻近的点相交，一条光线随机反射向光源，另一条光线则不会。反射向光源的光线会呈现出非常明亮的颜色。反射到其他地方的光线会呈现出非常暗的颜色。这两种光线的强度实际上应该处于中间位置。如果我们将这两条光线都引导向光源，就可以减轻这个问题，但这会导致场景亮度不准确。

  我们通常从相机中获取任意给定位置的光线，并投射到场景中，终于光源。但是反过来想想，如果我们从光源开始跟踪光线，穿过场景并终止于相机。该光线一开始会很明亮，并在场景中的每一次弹射时损失能量。它最终会进入相机，但会因为各种表面的反射而变暗并着色。现在，想象一下，如果这束光线被迫尽快向相机反弹。它会很变得很明亮且不太准确，因为它的能量没有被连续的反弹所消耗。这类似于向光源发送更多随机样本。这将在很大程度上解决我们明亮的像素旁边是较暗的像素的问题，但它只会让我们的所有像素都变亮。

  我们可以通过降低这些样本的权重来调整过度采样，从而消除这种不准确性。我们如何进行这种调整？好吧，我们首先需要了解概率密度函数的概念。但要理解概率密度函数的概念，我们首先需要知道密度函数是什么。

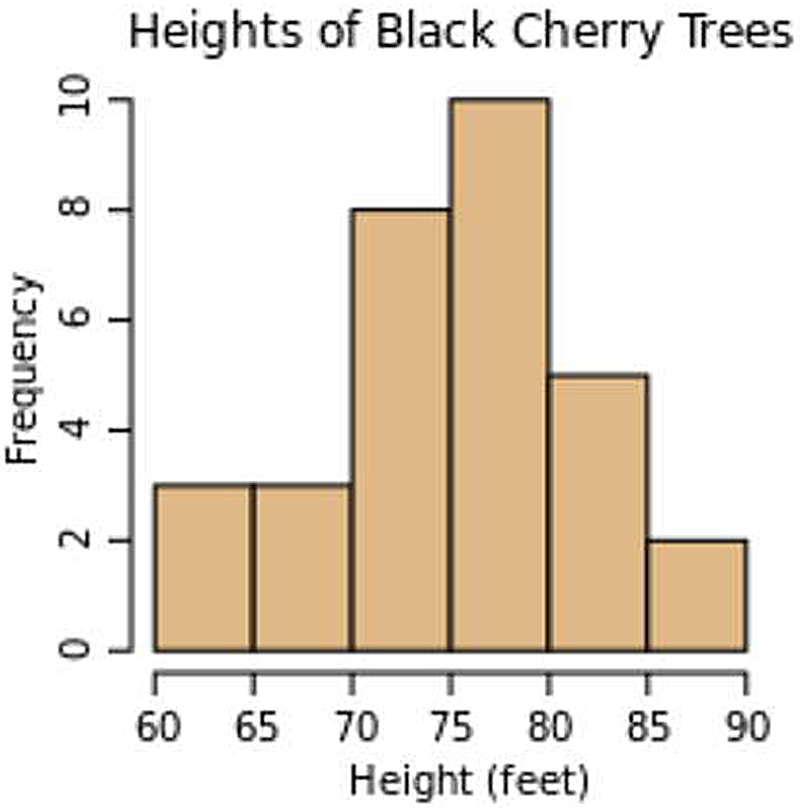
  密度函数只是直方图的连续版本。以下是直方图维基百科页面中的示例：

  如果在我们的数据源中，有更多的数据项，底部的划分区间保持不变，但是每个划分区间的频率会更高。如果我们把数据分成更多的区，则每个区间的频率会降低。如果我们让划分区间无限多，那么我们会得到无线多的零频率区间。为了解决这个问题，我们将用离散密度函数替换直方图（离散函数）。离散密度函数与离散函数的不同之处在于，它将频率$y$轴归一化为一个百分比，即密度。从离散函数转换为离散密度函数很简单：

$$Density\space of\space Bin\space i = \frac{Number\space of \space items \space in\space Bin \space i}{Number\space of \space items \space total}$$

  一旦我们有了离散密度函数，我们可以把离散值转换为连续值，将它转换为密度函数：

$$Bin\space Density = \frac{Fraction\space of \space tree \space between \space height \space H \space and \space H'}{H'-H}$$

  因此，密度函数是一个连续的直方图，其中所有值都根据总数进行归一化。如果我们有一棵特定的树，我们想知道它的高度，我们可以创建一个概率函数，它会告诉我们这棵树落入特定高度区间的可能性有多大。

$$Probability\space of \space Bin\space i = \frac{Number\space of \space items \space in\space Bin \space i}{Number\space of \space items \space total}$$

  如果我们把概率函数和我们（连续的）密度函数结合起来，我们可以将其解读为树高的一个统计预测指标：

$$Probability\space a\space random\space tree\space is\space between\space H\space and\space H′=Bin\space Density\space⋅(H−H′)$$

  事实上，有了这个连续的概率函数，我们现在可以说出任何给定树的高度将其置于多个划分区间的任意跨度内的可能性。这是一个概率密度函数（以下简称PDF）。简而言之，PDF是一个连续函数，可以对其进行积分以确定结果在某个区间中的概率。

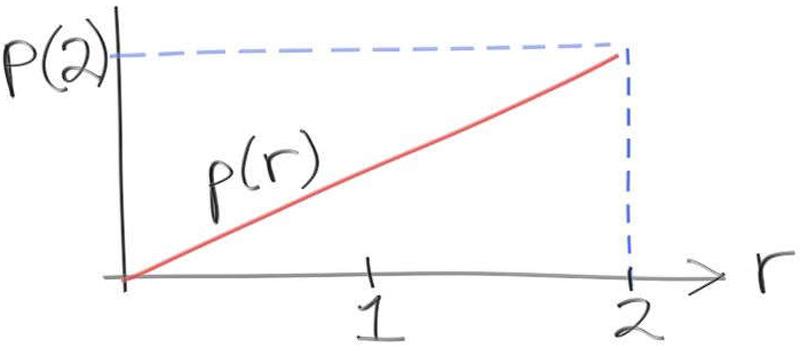
3.4. 构造PDF

  让我们构造一个PDF并尝试通过它来理解PDF。我们将使用下面这个函数：

  该函数做了什么呢？我们知道PDF只是一个连续函数，它定义了任意区间的概率。此函数$p(r)$限制在0到2之间，并沿着该区间线性增加。因此，如果我们使用此函数作为PDF来生成随机数，那么获得靠近0的数字的概率将小于获得靠近2的数字的概率。（译者注：PDF在0附近的积分面积小）

  PDF $p(r)$是一个线性函数，从$r=0$（$p(0)$）开始，并且单调增加到它的最高点$r=2$（$p(2)$）。$p(2)$的值是多少呢？$p(r)$呢？也许$p(2)$的值是2？PDF 从 0 线性增加到 2，因此猜测$p(2)$的值为2似乎是合理的。至少看起来它不可能是0。

  记住一点，PDF是概率函数。我们正在限制PDF，使其位于$[0,2]$范围内。PDF是表示一个列表的密度连续函数。如果我们知道该列表中的所有内容都包含在0 和2之间，我们可以说从该列表中取值在0到2之间的值的概率是$100%$。因此，曲线下的面积总和必须为1：

$$area(p(r),0,2) = 1$$

  所有线性函数可以被表示成一个常数乘以一个变量的形式：

$$p(r) = C\cdot r$$

  我们需要求解C的值。我们可以使用积分来反解：

$$\begin{align} 1 &= area(p(r),0,2)\\ &=\int_{0}^{2}C\cdot rdr\\ &=C\cdot\int_{0}^{2}rdr\\ &=C\cdot \frac{r^2}{2}|_0^2\\ &=C(\frac{2^2}{2}-\frac{0}{2})\\ & C = \frac{1}{2} \end{align}$$

  这表明，PDF是$p(r)=\frac{r}{2}$。就像直方图一样，我们可以对区域求和（积分），以计算出$r$在某个区间$[x_0,x_1]$的概率：

$$Probability(r|x_0 \leq r \leq x_1) = area(p(r),x_0,x_1)\\ Probability(r|x_0 \leq r \leq x_1) = \int_{x_0}^{x_1}\frac{r}{2}dr$$

  为了确认你已经清楚，你可以计算$r=0$到$r=2$的积分，这样就会得到概率1。

  在花费足够多的时间研究PDF之后，你可能会开始将PDF视为变量$r$为值$x$的概率，即$p(r=x)$

$$\begin{align} Probability(r=x) &= \int_x^xp(r)dr\\ &=P(r)|_x^x\\ &=P(x)-P(x)\\ &=0 \end{align}$$

   进一步推导，会发现，在$x$附近邻域内，概率不为0：

$$Probability(r|x-\Delta x < x + \Delta x)=area(p(r),x-\Delta x, x+ \Delta x)\\ =P(x+\Delta x) - P(x-\Delta x)$$

3.5. 选择我们的采样方法

  如果我们有我们关心的函数的PDF，那么我们就可以计算该函数在任意区间内返回一个值的概率。我们可以利用这一点来确定我们采样的范围。要记得这一点，最开始我们是为了确定对场景进行采样的最佳方式，这样我们就不会在非常暗的像素旁边得到非常亮的像素。如果我们有场景的PDF，那么我们可以按概率将样本引导到光线上，使渲染结果更加准确。前面提到过，如果我们将样本转向光线，那么我们将使图像产生不准确地亮点。我们需要弄清楚如何在不引入这种不准确的情况下引导我们的样本，这将在后面稍作解释，但现在如果我们有PDF，我们将专注于生成样本。我们如何使用PDF生成随机数？为此，我们需要更多的机制。别担心——这不会永远持续下去！

  我们随机数生成器random_double()生成一个在0到1之间的double。该数字生成器在0到1之间是均匀的，所以在0到1之间的任意数字都是等概率的。如果我们的PDF在定义域内也是均匀的，例如在0到10之间，那么我们可以为该PDF生成均匀的采样点：

10.0 * random_double()

  这是一个简单的例子，但我们将要关注的绝大多数情况都是不均匀的。我们需要一个方法将均匀的随机数生成器转换成非均匀的随机数生成器，且它的分布由指定的PDF定义。我们假设存在一个函数$f(d)$，它接受均匀分布的输入值并产生由PDF加权的非均匀分布。我们只需要想出一种方法来求解$f(d)$

  对于上面给出的PDF，即$p(r)=r^2$，随机样本接近2的概率高于接近0的概率。得到1.8到2.0之间的数字的概率比得到0.0到0.2 之间的数字的概率更大。如果我们暂时放下数学情节，从计算机科学的角度来思考，也许我们可以想出一种聪明的方法来划分PDF。我们知道，对于该PDF，在2附近的概率比在0附近的大，但是什么值会把概率分成一半呢？即什么值，有50%的概率会比它高，而另50%的概率比它低？为了求解该值，可以列如下方程：

$$50\%=\int_0^x\frac{r}{2}dr=\int_x^2\frac{r}{2}dr$$

  求解该方程，可以得到：

$$\begin{align} 0.5 &= \frac{r^2}{4}|_0^x\\ 0.5 &= \frac{x^2}{4}\\ x^2 &= 2\\ x &= \sqrt{2} \end{align}$$

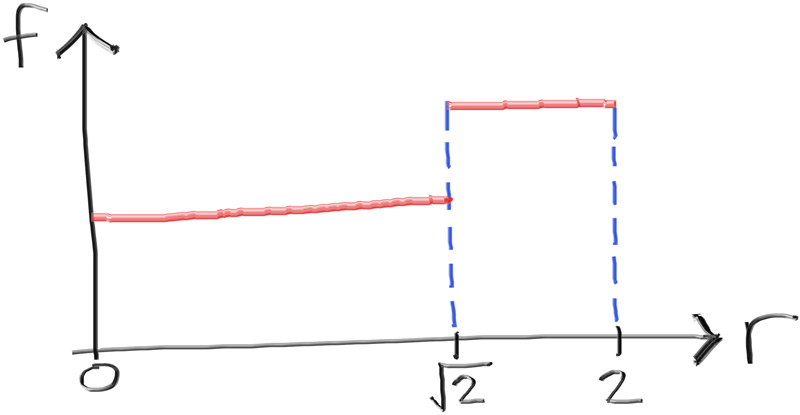
  作为一个粗略的近似值，我们可以创建一个函数f(d)，它以double d = random_double()为输入。如果d小于或等于0.5，它生成一个在$[0,\sqrt{2}]$内均匀分布的随机数，如果d大于0.5，它产生在$[\sqrt{2},2]$内均匀分布的随机数。

double f(double d)
{
    if (d <= 0.5)
        return std::sqrt(2.0) * random_double();
    else
        return std::sqrt(2.0) + (2 - std::sqrt(2.0)) * random_double();
}

  我们最初的随机数生成器是在0到1内均匀分布的：

  新的对$r^2$的近似函数是非均匀的（但局部均匀）：

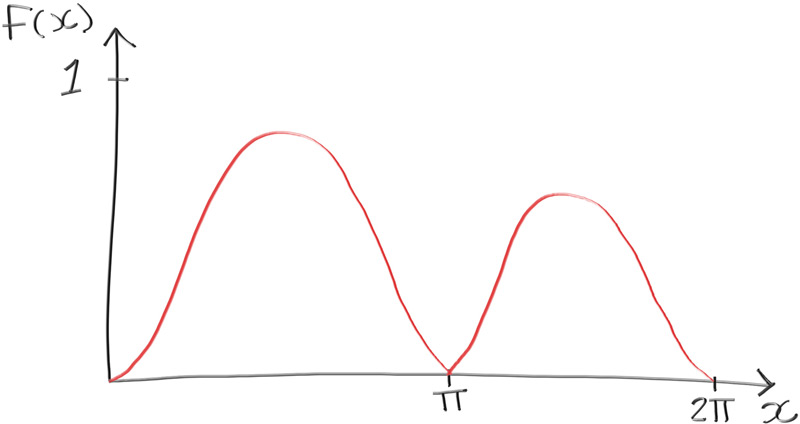
  我们有上述积分的分析方案，因此我们可以很容易地求解50%的概率。但我们也可以通过实验程序来求解这个50%的概率。有些函数我们要么不能，要么不想解它的积分。在这些情况下，我们也可以得到接近实际值的实验结果。让我们以下面这个函数为例来说明：

$$p(x)=e^{\frac{-x}{2\pi}}sin^2(x)$$

  该函数的图像如下：

  此时，你应该熟悉如何通过实验求解曲线下的面积。我们将使用现有代码并对其进行轻微修改，以获得50%概率的估计值。我们想要求解一个$x$的值，该值为曲线下总面积的一半。当我们连续求解$N$个样本的滚动和时，我们还将存储每个单独的样本及其 $p(x)$ 值。求解总和后，我们将对样本进行排序并将它们相加，直到我们的面积占总面积的一半。例如，从0到2π：

#include "rtweekend.h"

#include <algorithm>
#include <vector>
#include <iostream>
#include <iomanip>

struct sample {
    double x;
    double p_x;
};

bool compare_by_x(const sample& a, const sample& b) {
    return a.x < b.x;
}

int main() {
    const unsigned int N = 10000;
    sample samples[N];
    double sum = 0.0;

    // Iterate through all of our samples.

    for (unsigned int i = 0; i < N; i++) {
        // Get the area under the curve.
        auto x = random_double(0, 2*pi);
        auto sin_x = std::sin(x);
        auto p_x = exp(-x / (2*pi)) * sin_x * sin_x;
        sum += p_x;

        // Store this sample.
        sample this_sample = {x, p_x};
        samples[i] = this_sample;
    }

    // Sort the samples by x.
    std::sort(std::begin(samples), std::end(samples), compare_by_x);

    // Find out the sample at which we have half of our area.
    double half_sum = sum / 2.0;
    double halfway_point = 0.0;
    double accum = 0.0;
    for (unsigned int i = 0; i < N; i++){
        accum += samples[i].p_x;
        if (accum >= half_sum) {
            halfway_point = samples[i].x;
            break;
        }
    }

    std::cout << std::fixed << std::setprecision(12);
    std::cout << "Average = " << sum / N << '\n';
    std::cout << "Area under curve = " << 2 * pi * sum / N << '\n';
    std::cout << "Halfway = " << halfway_point << '\n';
}

  此代码片段与我们之前的代码片段没有太大区别。我们仍在求解一个区间（0 到 2π）的和。只是这一次，我们还将按输入和输出存储和排序所有样本。我们逐个叠加排序后的采样结果，来确定占整个区间面积总和一半的点。一旦我们知道我们的前$i$个样本的总和达到总和的一半，我们就知道第$i$个$x$大致对应于我们的中间点：

Average = 0.314686555791
Area under curve = 1.977233943713
Halfway = 2.016002314977

  如果你通过积分求解0到2.016以及2.016到2π的积分，你将会得到几乎一致的结果。

  我们有一种方法可以解决将PDF一分为二的中间点。如果我们愿意，我们可以使用它来递归地创建PDF的嵌套二进制分区（译者注：对二分点的左右两边区间多次划分）：

1. 求解PDF的二分点
2. 对小于二分点的一半区间，重复步骤1
3. 对高于二分点的一半区间，重复步骤1

  在合理的深度停下来，比如 6-10。很显然，这在计算上可能非常昂贵。上述代码的计算瓶颈可能是对样本进行排序。朴素排序算法的算法复杂度可能为$O(n^2)$时间，这非常昂贵。幸运的是，标准库中包含的排序算法通常更接近$O(nlog(n))$时间，但这仍然相当昂贵，尤其是对于数百万或数十亿个样本。但这将产生非均匀随机数的非均匀分布。这种产生非均匀分布的分而治之的方法在实践中有些普遍，尽管有比二分法更有效的方法。如果您有一个任意函数，希望将其用作发行版的PDF，则需要研究Metropolis-Hastings算法。

  译者注：这里取0.5的概率作为划分点，就是为了层层二分，选取出每一层二分点，用这些点来组成一个近似的分布函数。基于此，就可以构建一个基于均匀分布的近似分布的随机数生成器。只是在生成随机数的时候，要像抛硬币一样，来选取每一层左边区间和右边区间，直到叶子节点。

3.6. 近似分布（Approximating Distributions）

  本小节会有介绍大量的数学相关内容来构建一些概念。让我们回到最初的PDF。对于区间外的概率，我们假设PDF等于0。因此，对于章节开始的例子，有如下等式：

$$p(r)= \begin{cases} 0\quad r<0\\ \frac{r}{2}\quad 0\leq r \leq 2\\ 0\quad 2 < r \end{cases}$$

  如果你考虑一下我们在上一节中试图做的事情，很多数学都是围绕着从零开始的 累积 面积（或 累积 概率）展开的。如第二个例子中，使用的函数：

$$f(x)=e^{\frac{-x}{2\pi}}\sin^2(x)$$

  我们关心从0到2π的累积概率（100%）和从0到2.016的累积概率（50%）。我们可以将其归纳为一个重要的术语，累积分布函数$P(x)$ 定义如下：

$$P(x) = \int_{-\infin}^xp(x')dx'$$

  或者是下面的形式：

$$P(x) = area(p(x'),-\infin,x)$$

  这是从$-\infin$开始的累积概率量。由于微积分规则的原因，我们用 $x′$ 替代 $x$ 重写了积分。如果我们进行上述积分，将会得到分段函数：

$$P(r) = \begin{cases} 0\quad r < 0 \\ \frac{r^2}{4}\quad 0 \leq r \leq 2\\ 1\quad 2 < r \end{cases}$$

  概率密度函数（PDF）是解释在区间中选择数字的概率的函数。累积分布函数（CDF）解释的是小于输入值的区间中的狐族被选择的概率。从PDF到CDF，你需要从$-\infin$积分到 $x$ ，而从CDF到PDF，你需要求导：

$$p(x) = \frac{d}{dx}P(x)$$

  这表示从我们的PDF中提取的随机变量有25%的几率为1或更低。我们希望函数$f(d)$，输入一个在0-1之内服从均匀分布的值（例如$f(random_double())$，并且返回一个服从CDF $P(x) = \frac{x^2}{4}$的随机数。我们还不知道函数$f(d)$是什么，但我们确实知道它的返回值$25\%$应该小于$1.0$，$75%$应该高于1.0。这可以把$f(d)$定义为：

$$f(P(x))=x$$

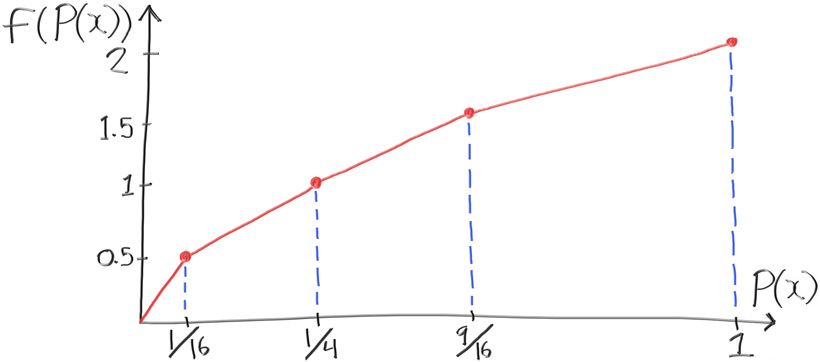
  让我们做一些采样：

$$P(0.0) = 0\\ P(0.5) = \frac{1}{16}\\ P(1.0) = \frac{1}{4}\\ P(1.5) = \frac{9}{16}\\ P(2.0) = 1$$

  因此，函数$f(d)$的值如下：

$$f(P(0.0)) = 0\\ f(P(0.5)) = \frac{1}{16}\\ f(P(1.0)) = \frac{1}{4}\\ f(P(1.5)) = \frac{9}{16}\\ f(P(2.0)) = 1$$

  我们可以利用这些中间值，并对它进行分段，来表示近似分布函数$f(d)$：

  如果你无法分析地求解PDF，那么你就无法分析地求解CDF。毕竟，CDF只是PDF的积分。然而，你仍然可以创建近似于PDF的分配。如果你从想要的PDF的随机函数中获取一组样本，则可以通过样本的直方图，将其转换为PDF来代表近似的PDF。或者，你可以像我们上面所做的那样，对所有样品进行排序。

  仔细观察下面的等式：

$$f(P(x))=x$$

  函数$f(d)$做着与$P(x)$相反的事情，因此函数$f(d)$是$P(x)$的反函数：

$$f(d) = P^{-1}(x)$$

  如果我们有了PDF $p(x)$和累积分布函数$P(x)$，我们可以使用”反函数”，以一个随机数为输入，来获取我们想要的值：

$$f(d) = P^{-1}(random\_double())$$

  对于我们的PDF $p(r) = \frac{r}{2}$，以及相应的$P(r)$，我们需要计算$P(r)$的反函数。假设$P(r)$如下：

$$y = \frac{r^2}{4}$$

  我们用$y$来表示$r$：

$$r = \sqrt{4y}$$

  这就是CDF的反函数（我们称其为$ICD(x)$），定义如下：

$$P^{-1}(r)=ICD(r)=\sqrt{4y}$$

  因此我们的随机数生成器可以定义如下：

$$ICD(d) = \sqrt{r\cdot random\_double()}$$

  注意，我们希望的返回值的范围是0到2，看看之前的分析，当random_double()返回$\frac{1}{4}$时，函数返回1，如果返回$\frac{1}{2}$时，函数返回$2-\sqrt{2}$，符合预期。

3.7. 重要性采样

  你现在应该对如何获取解析PDF并生成一个具有该分布的随机数的函数有一个很好的理解了。我们回到最初的积分，并使用不同的PDF以获得更好的理解：

$$I = \int_0^2x^2dx$$

  在前面，我们使用蒙特卡洛方法解这个积分，在0-2之间均匀地采样。我们当时并不知道，但我们隐含地使用了介于0和2之间满足均匀分布的PDF。 即在区间$[0,2]$内，PDF为$\frac{1}{2}$，CDF为$P(x) = \frac{x}{2}$，则$ICD(d) = 2d$。那么，我们可以使用该均匀分布的PDF改写程序如下：

#include "rtweekend.h"

#include <iostream>
#include <iomanip>

double icd(double d) {
    return 2.0 * d;
}

double pdf(double x) {
    return 0.5;
}

int main() {
    // int a = 0;
    // int b = 2;
    int N = 1000000;
    auto sum = 0.0;

    for (int i = 0; i < N; i++) {
        auto x = icd(random_double());
        sum += x*x / pdf(x);
    }
    std::cout << std::fixed << std::setprecision(12);
    std::cout << "I = " << (sum / N) << '\n';
}

  有几件重要的事情需要强调。$x$ 的每个值都表示分布$[0,2]$中函数$x^2$的一个样本。我们使用函数$ICD$从该分布中随机选择样本。我们之前是将区间 （sum / N） 乘以区间长度 （b - a） 的平均值来得出最终答案。在这里，我们不需要乘以区间长度，也就是说，我们不再需要将平均值乘以2。

  我们需要考虑 $x$ 的PDF的不均匀性。如果不考虑这种不均匀性，就会在我们的场景中引入偏差。事实上，这种偏差是我们图像中噪点的来源。考虑不均匀性将产生准确的结果。PDF将样本“引导”到分布的特定部分，这将使我们更快地收敛，但代价是引入偏差。为了消除这种偏差，我们需要在采样频率较高的区域降低权重，在采样频率较低的区域增加权重。对于我们新的非均匀随机数生成器，PDF定义了我们对特定部分的采样量。所以权值函数应该与$\frac{1}{pdf}$成正比。事实上，就是$\frac{1}{pdf}$。这也就是我们为什么让x*x除以$pdf(x)$。

  我们可以尝试求解该积分，使用线性PDF，$p(r)=\frac{r}{2}$，并求解它的CDF和ICD。为此，我们需要做的就是使用$ICD(d) = \sqrt{4d}$和$p(x)=\frac{x}{2}$进行替换：

double icd(double d) {
    return std::sqrt(4.0 * d);
}

double pdf(double x) {
    return x / 2.0;
}

int main() {
    int N = 1000000;
    auto sum = 0.0;

    for (int i = 0; i < N; i++) {
        auto z = random_double();
        if (z == 0.0)  // Ignore zero to avoid NaNs
            continue;

        auto x = icd(z);
        sum += x*x / pdf(x);
    }

    std::cout << std::fixed << std::setprecision(12);
    std::cout << "I = " << sum / N << '\n';
}

  如果你比较均匀分布的PDF和线性PDF，你会发现线性PDF收敛更快。理论上也很明显，线性PDF比均匀分布的PDF，更接近二次函数，因此收敛更快。如果是这样的话，那么我们应该尝试通过将PDF转换为二次函数来使PDF匹配被积函数:

$$p(r)= \begin{cases} 0\quad r < 0\\ C\cdot r^2\quad 0 \leq r \leq 2\\ 0\quad 2 < r \end{cases}$$

  和线性函数类似，我们要通过将在区间上的积分结果设为1来求解常数$C$：

$$\begin{align} 1 &= \int_0^2C\cdot r^2dr\\ &=C\cdot\int_0^2 r^2dr\\ &=C\cdot \frac{r^3}{3}|_0^2\\ &=C(\frac{2^3}{3}-\frac{0}{3})\\ C &= \frac{3}{8} \end{align}$$

  这就得到：

$$p(r) = \begin{cases} 0\quad r < 0\\ \frac{3}{8}r^2\quad 0 \leq r \leq 2\\ 0\quad 2 < r \end{cases}$$

  然后可以得到相应的CDF：

$$P(r) = \frac{r^3}{8}$$

  以及ICD：

$$P^{-1}(x)=ICD(d)=2d^{\frac{1}{3}}$$

  只需要一次采样，我们便可得到：

  译者注：原文这里推导 ICD 是不正确的。应该是2，但是原文是 8。而这里为什么8和2都一样，因为 ICD已经不重要了。具体可以阅读 Github 上相关的 Issue

double icd(double d) {
    return 2.0 * std::pow(d, 1.0/3.0);
}

double pdf(double x) {
    return (3.0/8.0) * x*x;
}

int main() {
    int N = 1;
    auto sum = 0.0;

    for (int i = 0; i < N; i++) {
        auto z = random_double();
        if (z == 0.0)  // Ignore zero to avoid NaNs
            continue;

        auto x = icd(z);
        sum += x*x / pdf(x);
    }
    std::cout << std::fixed << std::setprecision(12);
    std::cout << "I = " << sum / N << '\n';
}

  这始终返回确切的答案。

  非均匀的PDF会将更多样本“引导”到PDF较大的位置，而将较少的样本“引导”到PDF较小的位置。通过这种采样方式，我们预期PDF较大的地方噪声较少，而PDF较小的地方噪声较多。如果我们在场景中噪点较多的部分选择较高的PDF，而在场景中早点较少的部分选择较小的PDF，我们将能够使用较少的样本来达到降噪的目的。这意味着我们将能够比使用均匀的PDF更快地收敛到正确的场景。实际上，我们正在将样本引导到分布中更重要的部分。这就是通常所说的重要性采样，重要性采样要求仔细选择非均匀的PDF。

  在给出的例子中，我们总是能收敛到正确答案：$\frac{8}{3}$。我们得到相同的答案，当我们使用均匀的PDF和“正确”的PDF（即 $ICD(d)=2d^{\frac{1}{3}}$）。我们都收敛到相同的答案，但是均匀的PDF需要更长的时间。毕竟，后者只需要一次采样即可完美匹配积分结果。这应该是有道理的，因为我们选择更频繁地对分布的重要部分进行采样，而均匀的PDF只是对整个分布进行平等采样，而不考虑重要性。

  事实上，你创建的任何PDF都是这种情况——它们最终都会收敛。这只是Monte Carlo算法功能的另一个部分。即便是朴素的PDF，我们求解它50%概率的位置，把分布函数分成两个区间：$[0,\sqrt{2}]$和$[\sqrt{2},2]$。该PDF也会收敛。希望你能有一种直觉，为什么该PDF会比纯均匀PDF收敛得更快，但比线性PDF收敛得更慢（即$ICD(d)=\sqrt{4d}$）。

  完美的重要性采样只有在我们知道答案的情况下才能找到（能够从$p(x)$中积分得到分布函数$P(x)$），但这是确保我们的代码正常工作的好练习。

  让我们回顾一下Monte Carlo光线跟踪渲染器的主要概念：

1. 你有一个在某个域$[a,b]$上$f(x)$的积分。
2. 你选择了一个PDF $p(x)$，在$[a,b]$内非0且非负。
3. 你计算了大量的$\frac{f(r)}{p(r)}$的平均值，其中$r$是一个服从PDF $p(x)$所定义的分布的随机数。

  任意一个PDF $p(x)$都会收敛到正确答案，但是$p$越接近$f(x)$，收敛越快。

4. 方向球上的Monte Carlo积分

  在’一维蒙特卡罗积分’这一章中，我们从一个均匀随机数开始，慢慢地构造了越来越复杂的生成随机数的方式，然后最终解释了PDF，以及如何使用它们来生成任意分布的随机数。

  该章中涵盖的所有概念在我们单个维度中仍然有效。继续往前，我们将会从二维，三维或者更高维度空间中选择一个点，并使用任意的PDF来表示选择的权重。这方面的一个重要例子——至少对于光线追踪来说——就是产生随机的方向。在前两本书中，我们通过创建一个随机向量来生成一个随机方向，拒绝那些落在球体之外的向量。我们重复这个过程，直到找到一个落在单位球体内的随机向量。归一化此向量会生成正好位于单位球体上的点，从而表示随机方向。这种生成样本并在样本不在所需空间内时拒绝它们的过程称为拒绝法，在文献中随处可见。上一章中介绍的方法被称为反转方法，因为我们反转了PDF（PDF的倒数）。

  在3D空间中的每一个方向都有一个在单位球上的关联点并且可以通过计算从球心到该点的方向来生成它。你可以将选择随机方向视为在受约束的二维平面中选择一个随机点：通过将单位球体映射到笛卡尔坐标而创建的平面。与以前使用的方法相同，但现在我们可能在两个维度上定义了PDF。假设我们想在单位球体的表面上对这个函数进行积分：

$$f(\theta,\phi)=cos^2(\theta)$$

  使用蒙特卡洛积分，我们应该采样$\frac{cos^2(\theta)}{p(r)}$，其中$p(r)$现在是$p(direction)$。但是在这种情况下，什么是方向？我们可以使用极坐标来定义它，所以$p$会被写成$\theta$和$\phi$的形式：$p(\theta,\phi)$。用什么坐标系统无关紧要。尽管如此，无论您选择如何操作，请记住在整个表面上与PDF积分必须为1，并且PDF代表该方向被采样的相对概率 。回想一下，我们有一个vec3函数，可以在单位球体（random_unit_vector()） 上生成均匀的随机样本。这些均匀的随机样本的PDF是什么呢？作为单位球面上的均匀密度，PDF是$\frac{1}{球体表面积}$，即$\frac{1}{4\pi}$。如果被积函数是$cos^2(\theta)$，$\theta$是与$z$轴的角度，我们可以使用标量投影将$cos^2(\theta)$改写为$d_z$的形式：

$$d_z = ||d||cos\theta = 1\cdot cos\theta$$

  我们可以用$d_z$代替 $1\cdot cost \theta$ 代入公式：

$$f(\theta,\phi)=cos^2(\theta)={d_z}^2$$

#include "rtweekend.h"

#include <iostream>
#include <iomanip>

double f(const vec3& d) {
    auto cosine_squared = d.z()*d.z();
    return cosine_squared;
}

double pdf(const vec3& d) {
    return 1 / (4*pi);
}

int main() {
    int N = 1000000;
    auto sum = 0.0;
    for (int i = 0; i < N; i++) {
        vec3 d = random_unit_vector();
        auto f_d = f(d);
        sum += f_d / pdf(d);
    }
    std::cout << std::fixed << std::setprecision(12);
    std::cout << "I = " << sum / N << '\n';
}

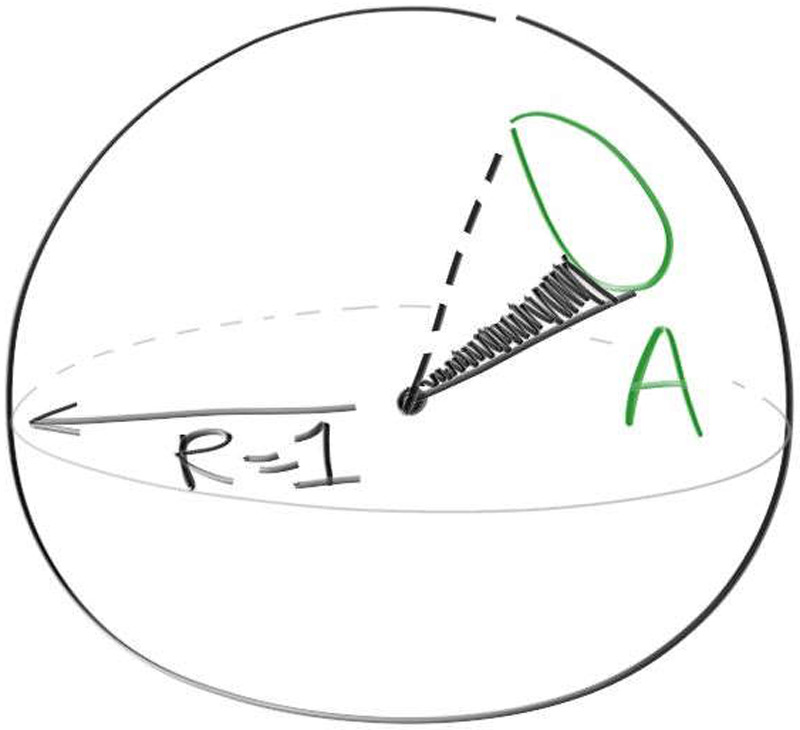
  答案是$\frac{4}{3}\pi=4.188790204786391$——如果你记得足够多的高级计算，帮我验算一下！上面的代码生成了这一点。这里的关键点是所有的积分和概率以及其他一切都在单位球面上。在3D空间中表示单个方向的方法是找到它在单位球体上的关联点。在3D中表示方向范围的方法是这些方向行进的单位球体上的面积。把它称为方向，面积或立体角（solid angle）——都是一样的东西。立体角是你将会经常在文献里看到的名词。在一维上，有弧度(r) $\theta$，在二维上，有球面度(sr) $\theta$ 和 $\phi$（单位球是三维物体，但是它的表面只有二维，很好！）。立体角只是角度的二维扩展。如果您对二维角度有一定的理解，那就太好了！如果没有，就按照我所做的，想象一组方向穿过的单位球体上的区域。立体角$\omega$和单位球面上的投影面积$A$是一回事。

  现在让我们继续求解的光传输方程。

5. 光的散射

  在本章中，我们不会实际进行编码。我们将在下一章中为大的照明变化做准备。前两本书中的光线追踪程序在光线与表面或体积交互时对其进行散射。光线散射是模拟光线在场景中传播的最常用模型。这自然可以进行概率建模。在对射线的概率散射进行建模时，需要考虑很多事情。

5.1. 反照率（Albedo）

  首先第一点，就是光线是否被吸收？

  如果光线散射的概率: A，那么光线被吸收的概率为1-A

  这里A指的就是反照率（Albedo）。在我们第一本书中，复习一下反照率是反射比例的一种形式。停下来复习，让前面的知识更加巩固，当我们模拟光的传播时，我们所做的只是模拟光子在空间中的运动。如果你记得高中学过的物理知识，就重温一下，根据普朗克常数，每一个光子都有唯一的能量和波长：

$$E = \frac{hc}{\lambda}$$

  每一个独立的光子都有微小的能量，在渲染过程中，当你把它们加起来累积到足够多时，你会在渲染中获得所有的照明。光子在与物体表面或体积内（或任何可以与光子交互的物体）交互时，表现出的吸收和散射的特性，该特性就是物体本身的反照率。

  在大多数基于物理的渲染中，我们将为光的颜色使用一组预定义的特定波长，而不是 RGB。例如，我们将用专门在300nm、350nm、400nm、…、700nm 采样的东西替换我们的三原色RGB渲染器。我们可以通过将R、G和B视为波长的特定代数混合物来扩展我们的直觉，其中R是红色波长，G是绿色波长，B是蓝色波长。这是人类视觉系统的近似值，它有3组独特的颜色感受器，称为视锥细胞，每组颜色受体对不同的波长代数混合物敏感，大致为RGB，但被称为长、中和短视锥细胞（这些名称是指每个视锥细胞感光的光波长区间，而不是视锥细胞的长度）。正如颜色可以用它们在RGB色彩空间中的强度来表示一样，颜色也可以用每组视锥细胞在LMS 色彩空间（长、中、短）中的敏感程度来表示。

5.2. 散射

  如果光发生散射，它将具有基于方向的分布，我们可以将其描述为立体角上的 PDF。我将它称为散射PDF:$pScatter()$。散射PDF将随出射方向而变化：$pScatter(\omega_o)$。散射PDF也随入射方向变化：$pScatter(\omega_i,\omega_o)$。当您查看道路的反射时，你可以看到它随入射方向而变化——当您的视线（入射角）接近反射光线时，它们会变得像镜子一样。散射PDF还会随光的波长而变化：$pScatter(\omega_i, \omega_o, \lambda)$。一个很好的例子是将白光折射成彩虹的棱镜。最后，散射PDF也可以取决于散射位置：$pScatter(x, \omega_i,\omega_o,\lambda)$。$x$只是散射位置的数学符号：$x=(x,y,z)$。物体的反照率也可以取决于这些量：$A(x,\omega_i,\omega_o,\lambda)$。

  表面的颜色是按入射方向在单位半球上对这些项进行积分得到的：

$$Color_o(x,\omega_o,\lambda)=\int_{\omega_i}A(x,\omega_i,\omega_o,\lambda)\cdot p Scatter(x,\omega_i,\omega_o,\lambda)\cdot Color_i(x,\omega_i,\lambda)$$

  我们添加了一个$Color_i$的术语。散射PDF和物体表面的反照率充当照射在该点上的光的过滤器。因此，我们需要求解照射在那个点上的光。这是一种递归算法，也是我们的ray_color函数返回当前物体的颜色乘以下一条光线的颜色的原因

5.3. 散射PDF

  如果我们应用蒙特卡洛基本公式，我们会得到以下统计估计：

$$Color_o(x,\omega_o,\lambda)\approx\sum\frac{A(...)\cdot p Scatter(...) \cdot Color_i(...)}{p(x,\omega_i,\omega_o,\lambda)}$$

  其中$p(x,\omega_i,\omega_o,\lambda)$是我们随机生成的任意出射方向的PDF。

  对于Lambertian表面，我们已经为pScatter(...)是余弦密度的特殊情况隐式实现了这个公式。Lambertian表面的$pScatter(…)$与$\cos(\theta_o)$成正比，其中$\cos(\theta_o)$是出射光线相对于表面法线的夹角（$\theta_o\in [0,\pi]$）。0度角表明出射光线与表面法线通向，而$\pi$表明出射光线的方向正好与表面法线相反。

  让我们再次求解常数$C$：

$$pScatter(x,\omega_i,\omega_o,\lambda)=C\cdot cos(\theta_0)$$

  PDF的在整个表面上的积分结果为1。我们让$pScatter(\frac{\pi}{2} < \theta_o \leq \pi) = 0$，这样我们就不会散射到水平面以下。由此，我们只需要在$\theta \in [0,\frac{\pi}{2}]$区间上积分：

$$1 = \int_{\phi=0}^{2\pi}\int_{\theta=0}^{\frac{\pi}{2}}C\cdot cos(\theta)dA$$

  要在半球上积分，记得转换到球面坐标系：

$$dA = sin(\theta)d\theta d\phi$$

  由此可得：

$$1 = C\cdot \int_{0}^{2\pi}\int_{0}^{\frac{\pi}{2}}cos(\theta)sin(\theta)d\theta d\phi\\ 1 = C \cdot 2\pi \frac{1}{2}\\ 1 = C \cdot \pi\\ C = \frac{1}{\pi}$$

  在半球面上，$\cos(\theta)$的积分结果是$\pi$，所以我们需要使用$\frac{1}{\pi}$来进行归一化。PDF $pScater$只依赖于出射光线（$\omega_o$），所有我们可以使用$pScatter(\omega_o)$化简前面的公式。把所有东西归纳到一起，得到Lanbertian表面的散射PDF为：

$$pScatter(\omega_0)=\frac{cos(\theta_0)}{\pi}$$

  我们假设$p(x,\omega_i,\omega_o,\lambda)$和散射PDF相等：

$$p(\omega_0)=pScatter(\omega_0)=\frac{cos(\theta_0)}{\pi}$$

  消去分子和分母，可得：

$$Color_0(x,\omega_0, \lambda) \approx \sum A(...)\cdot Color_i(...)$$

  这就是最初我们原来的ray_color()函数：

return attenuation * ray_color(scattered, depth-1, world);

  上面的处理稍微不标准，因为我希望相同的数学方法也适用于表面和体积。如果你阅读文献，你会发现反射都是由双向反射分布函数定义的（BRDF）。它与我们的公式中的每一项很相似：

$$BRDF(\omega_i,\omega_o,\lambda)=\frac{A(x,\omega_i,\omega_o,\lambda)\cdot pScatter(x,\omega_i,\omega_o,\lambda)}{cos(\theta_0)}$$

  因此，以Lambertian表面为例，$BRDF = \frac{A}{\pi}$。在我们的术语和BRDF之间转换很容易。对于参与介质（体积），我们的反照率通常称为 散射反照率，而我们的散射PDF通常称为相位函数。

  我们在这里所做的只是描述了Lambertian材质散射的PDF。但是，我们需要进行泛化，以便我们可以在重要方向上发送额外的光线，例如朝向灯光。

6. 尝试重要性采样

  在接下来的几章中，我们的目标是对原来的程序代码进行改进，向光源发送一堆额外的光线，从而减少图片的噪点。假设我们可以使用PDF将一束光线发送到光源$pLight(\omega_o)$。我们还假设我们有一个与pScatter相关的PDF，我们将其命名为$pSurface(\omega_o)$。PDF的一大优点是，你可以对它们的进行线性混合，得到的结果也是 PDF，即混合概率密度函数。例如，最简单的混合是：

$$p(\omega_o) = \frac{1}{2}pSurface(\omega_o)+\frac{1}{2}pLight(\omega_o)$$

  只要权值是正数且相加结果为1，所有这些PDF的线性叠加结果也是一个PDF。记住，我们可以使用任何PDF：所有的PDF最终都会收敛到正确答案。所以，目标是要弄清楚在下面的乘积中最大的位置，如何使PDF更大一些（译者注：结合PDF的概念和拟合答案的逻辑，这里指的是在乘积结果较大的地方，PDF应该越大，这样越容易接近目标）：

$$pScatter(x,\omega_i,\omega_o)\cdot Color_i(x,\omega_i)$$

  对于漫反射表面，这主要是的问题是在什么位置$Color_i(x,\omega_i)$最大。这相当于在问最多的光来自何方。

  对于镜面，$pScatter()$只在一个方向上非常大，所以$pScatter()$更重要。实际上，大多数渲染器只是将镜像作为一种特殊情况，并使$\frac{pScatter()}{p()}$ 成为隐式的——我们的代码目前也是这样做的。

6.1. 回到康奈尔盒子

  让我们对Cornell Box场景的参数稍微做一些修改：

int main() {
    ...
    cam.samples_per_pixel = 1000;
    ...
}

  600x600的分辨率，代码在我1核的Macbook上运行了15分钟，得出如下结果：

  我们的目标是减少这些噪点。我们会通过构造PDF，并发射更多朝向光源的光线来达到这一目的。

  首先，让我们修改代码，以便它显式地对一些PDF进行采样，然后进行归一化。记住Monte Carlo的基本知识：$\int f(x)\approx \sum \frac{f(r)}{p(r)}$。对于Lambertian材质，然我们按上一节中推导的那样进行采样：$p(\omega_o)=\frac{\cos(\omega_o)}{\pi}$。
  我们修改基类material来开始实现重要性采样的逻辑，然后为Lambertian材质定义散射PDF函数：

class material {
  public:
    ...

    virtual double scattering_pdf(const ray& r_in, const hit_record& rec, const ray& scattered)
    const {
        return 0;
    }
};

class lambertian : public material {
  public:
    lambertian(const color& albedo) : tex(make_shared<solid_color>(albedo)) {}
    lambertian(shared_ptr<texture> tex) : tex(tex) {}

    bool scatter(const ray& r_in, const hit_record& rec, color& attenuation, ray& scattered)
    const override {
        ...
    }

    double scattering_pdf(const ray& r_in, const hit_record& rec, const ray& scattered)
    const override {
        auto cos_theta = dot(rec.normal, unit_vector(scattered.direction()));
        return cos_theta < 0 ? 0 : cos_theta/pi;
    }

  private:
    shared_ptr<texture> tex;
};

  camera::ray_color函数也做一些微小的改变：

class camera {
  ...
  private:
    ...
    color ray_color(const ray& r, int depth, const hittable& world) const {
        // If we've exceeded the ray bounce limit, no more light is gathered.
        if (depth <= 0)
            return color(0,0,0);

        hit_record rec;

        // If the ray hits nothing, return the background color.
        if (!world.hit(r, interval(0.001, infinity), rec))
            return background;

        ray scattered;
        color attenuation;
        color color_from_emission = rec.mat->emitted(rec.u, rec.v, rec.p);

        if (!rec.mat->scatter(r, rec, attenuation, scattered))
            return color_from_emission;

        double scattering_pdf = rec.mat->scattering_pdf(r, rec, scattered);
        double pdf_value = scattering_pdf;

        color color_from_scatter =
            (attenuation * scattering_pdf * ray_color(scattered, depth-1, world)) / pdf_value;

        return color_from_emission + color_from_scatter;
    }
};

  你将会得到相同的图像。这很好理解，因为ray_color中散射的部分乘上了系数scattering_pdf/pdf_value，而pdf_value与scattering_pdf相等，这相当于乘上了1。

6.2. 使用均匀分布的PDF代替完美匹配

  现在，仅仅是为了实验，让我们尝试使用不同的采样PDF。我们还是继续使用Lambertian材质计算反射光线，即$cos(\theta_o)$，并且让散射PDF与之前一样，但是使用不同的PDF作为分母。我们将会使用在半球上均匀分布的PDF，所以分母是$\frac{1}{2\pi}$。这仍然会收敛到正确的答案，因为我们只是修改了PDF，但是由于均匀分布的PDF与实际的分别不太匹配，所以它需要更长的时间才会收敛。这样依赖，相同的采样次数会产生更多的噪点：

class camera {
  ...
  private:
    ...
    color ray_color(const ray& r, int depth, const hittable& world) const {
        hit_record rec;

        // If we've exceeded the ray bounce limit, no more light is gathered.
        if (depth <= 0)
            return color(0,0,0);

        // If the ray hits nothing, return the background color.
        if (!world.hit(r, interval(0.001, infinity), rec))
            return background;

        ray scattered;
        color attenuation;
        color color_from_emission = rec.mat->emitted(rec.u, rec.v, rec.p);

        if (!rec.mat->scatter(r, rec, attenuation, scattered))
            return color_from_emission;

        double scattering_pdf = rec.mat->scattering_pdf(r, rec, scattered);
        double pdf_value = 1 / (2*pi);

        color color_from_scatter =
            (attenuation * scattering_pdf * ray_color(scattered, depth-1, world)) / pdf_value;

        return color_from_emission + color_from_scatter;
    }

  你应该得到与之前非常相似的结果，只是噪点稍微多一点，可能很难看出来。

  确保使用的PDF是散射PDF：

...
double scattering_pdf = rec.mat->scattering_pdf(r, rec, scattered);
double pdf_value = scattering_pdf;
...

6.3. 随机半球采样

  为了确保我们确实理解了这些内容，让我们尝试不同的散射分布。对于这一章的内容，我们将会再一次使用第一本书中使用的均匀半球散射。这种技术没有错，但我们不再将我们的物体视为Lambertian的。Lambertian是一种特殊的漫反射材质，它需要$\cos(\theta_o)$的散射分布。均匀的半球散射也是一种不同的漫反射材质。如果我们保持材质一致，但是改变PDF，就像上一节做的那样，我们仍然会收敛到相同的答案，但是收敛需要更多的样本。但是，如果我们改变材质，我们将从根本上改变渲染，算法将收敛于不同的答案。所以，当我们用均匀半球漫反射替换Lambertian漫反射时，由于材质的改变，我们得到“实质上地”不同的渲染结果。我们改变散射方向和散射PDF：

class lambertian : public material {
  public:
    lambertian(const color& albedo) : tex(make_shared<solid_color>(albedo)) {}
    lambertian(shared_ptr<texture> tex) : tex(tex) {}

    bool scatter(const ray& r_in, const hit_record& rec, color& attenuation, ray& scattered)
    const override {
        auto scatter_direction = random_on_hemisphere(rec.normal);

        // Catch degenerate scatter direction
        if (scatter_direction.near_zero())
            scatter_direction = rec.normal;

        scattered = ray(rec.p, scatter_direction, r_in.time());
        attenuation = tex->value(rec.u, rec.v, rec.p);
        return true;
    }

    double scattering_pdf(const ray& r_in, const hit_record& rec, const ray& scattered)
    const override {
        return 1 / (2*pi);
    }

    ...

  新的漫反射材质散射PDF为$p(\omega_o)=\frac{1}{2\pi}$。所以我们的均匀分布的PDF与Lambertian漫反射并不是完美匹配，实际上它与均匀半球漫反射完美匹配。当渲染结束后，会得到一张略微不同的图像：

  它与旧图像比较相似，然而还是有一些区别，不仅仅是噪点。高箱子的正面颜色更加均匀。如果你无法确定你的材质的最佳采样是什么形式的，那么比较合理的方法就是将它假设为均匀分布的PDF，虽然它收敛得很慢，但是不会把渲染器搞崩。也就是说，在你无法确定的时候，PDF的选择不该是你优先考虑的问题，相比之下，散射函数的正确性才是确保渲染结果正确的首要条件，因为当散射函数不正确时，会产生不正确的结果。你可能会发现自己遇到了Monte Carlo程序中最难发现的Bug—— 一个产生看起来“合理”的图像的Bug ！你很难判断该Bug是第一个版本的程序引起的，还是第二个，或者两者皆有。

  让我们想一些办法来解决这个问题。

7. 生成随机方向

  在这一章和接下来的两章中，我们将强化我们的理解和我们的工具。

7.1. 相对于Z轴的随机方向

  让我们首先弄清楚如何生成随机方向。我们已经有了一个使用拒绝法生成随机方向的方法，所以让我们使用倒置法创建一个。为了方便，假设 $z$ 轴是表面法线，$\theta$是与法线的角度。本章我们将围绕$z$轴来讨论，下一章我们将让它们定向到表面法向量。我们只会处理绕 $z$ 旋转对称的分布。所以$p(\omega)=f(\theta)$ 。

  给定球面上的方向PDF（其中$p(\omega)=f(\theta)$），$\theta$和$\phi$上的一维PDF为（译者注：$b(\theta)$不太好理解，好像是在与 z 轴夹角为 θ 的锥形底部圆形上取随机方向。从极坐标系的角度来考虑，也不太清楚，只能凭直觉了。）：

$$a(\phi)=\frac{1}{2\pi}\\ b(\theta)=2\pi f(\theta)\sin(\theta)$$

  对于服从均匀分布的随机数$r_1$和$r_2$，我们求解$\theta$和$\phi$的CDF，以便于我们可以计算ICDF，构造新的随机数生成器。d

$$\begin{align} r_1 &= \int_0^{\phi}a(\phi ')d\phi '\\ &= \int_0^{\phi}\frac{1}{2\pi}d\phi '\\ &= \frac{\phi}{2\pi} \end{align}$$

  反解 $\phi$ 可得：

$$\phi = 2\pi\cdot r_1$$

  这与直觉相符。要获得一个随机的$\phi$，可以先生成一个在区间$[0,1]$内均匀分布的随机数然后乘上$2\pi$来覆盖$\phi$所有可能得值，即区间$[0,2\pi]$。对于如何求解$\theta$的随机值，你可能没有形成完全的直觉，所以让我们来通过一些数学运算来帮助你。我们用$\phi’$代替$\phi$，$\theta’$代替$\theta$。对于$\theta$，有：

$$\begin{align} r_2 &= \int_0^{\theta}b(\theta ')d\theta '\\ &= \int_0^{\theta}2\pi f(\theta')\sin(\theta')d\theta ' \end{align}$$

  让我们尝试一些不同的函数$f()$。让我们先尝试在在球形上的均匀分布。单位球的面积是$4\pi$，所以在球体上均匀分布的$p(\omega)$是$\frac{1}{4\pi}$。

$$\begin{align} r_2 &= \int_0^{\theta}2\pi\frac{1}{4\pi}\sin(\theta ')d\theta '\\ &= \int_0^{\theta}\frac{1}{2}\sin(\theta ')d\theta '\\ &= \frac{-\cos(\theta)}{2} - \frac{-\cos(0)}{2} \end{align}$$

  求解$\cos(\theta)$可得：

$$\cos(\theta)=1-2r_2$$

  我们并不需要求解$\theta$，因为我们只需要知道$\cos(\theta)$即可，也不需要在运行过程中调用$\arccos()$。

  为了生成以$(\theta,\phi)$定义的单位向量，我们将它转换到笛卡尔坐标系：

$$x = \cos(\phi)\cdot \sin(\theta)\\ y = \sin(\phi)\cdot \cos(\theta)\\ z = \cos(\theta)$$

  利用$\cos^2 + \sin^2 = 1$的性质，我们可以基于上面的推导，得到下面关于随机数$(r_1,r_2)$的等式：

$$x = \cos(2\pi\cdot r_1)\sqrt{1-(1-2r_2)^2}\\ y = \sin(2\pi\cdot r_1)\sqrt{1-(1-2r_2)^2}\\ z = 1-2r_2$$

  再简化一点，$(1-2r_2)^2=1-4r_2+4r_2^2$，所以：

$$x = \cos(2\pi r_1)\cdot 2\sqrt{r_2(1-r_2)}\\ y = \sin(2\pi r_1)\cdot 2\sqrt{r_2(1-r_2)}\\ z = 1-2r_2$$

  然后，我们可以输出一些内容了：

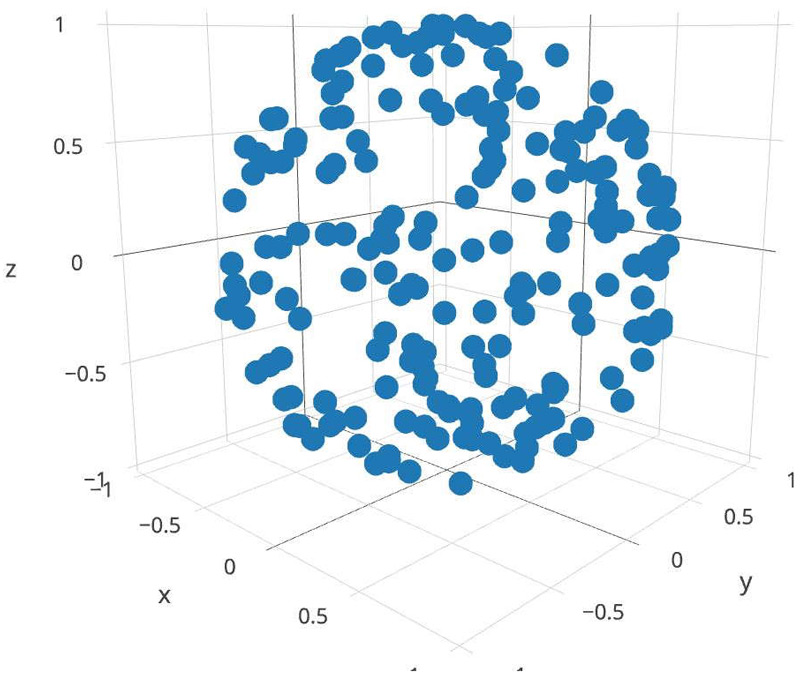
#include "rtweekend.h"

#include <iostream>
#include <math.h>

int main() {
    for (int i = 0; i < 200; i++) {
        auto r1 = random_double();
        auto r2 = random_double();
        auto x = std::cos(2*pi*r1) * 2 * std::sqrt(r2*(1-r2));
        auto y = std::sin(2*pi*r1) * 2 * std::sqrt(r2*(1-r2));
        auto z = 1 - 2*r2;
        std::cout << x << " " << y << " " << z << '\n';
    }
}

  并在 plot.ly（一个支持 3D 散点图的出色网站）上免费绘制它们：

  在 plot.ly 网页上，你可以旋转它，并可以看到它的分布很均匀。

7.2. 均匀半球采样

  现在，让我们继续尝试在半球上的均匀采样。在半球上均匀采样的密度意味着$p(\omega)=f(\theta)=\frac{1}{2\pi}$。仅仅只是修改了方程中的一个常量：

$$\begin{align} r_2 &= \int_0^{\theta}b(\theta ')d\theta '\\ &= \int_0^{\theta}2\pi f(\theta ')\sin(\theta ')d\theta'\\ &= \int_0^{\theta}2\pi \frac{1}{2\pi}\sin(\theta')d\theta'\\ &\quad\quad\quad\quad\quad...\\ &\quad\quad\cos(\theta) = 1-r_2 \end{align}$$

  这意味着$\cos(\theta)$的值将从1变化到0，因此θ将从0变化到$\frac{\pi}{2}$变化，这意味着没有任何东西会低于水平面。我们不是绘制它，而是用已知解求解二维积分。让我们对半球上的余弦立方进行积分（只需选择具有已知解的任意对象）。首先，我们将手动求解积分：

$$\begin{align} &\quad\space\int_\omega \cos^3(\theta)dA\\ &=\int_0^{2\pi}\int_0^{\frac{\pi}{2}}\cos^3(\theta)\sin(\theta)d\theta d\phi\\ &=2\pi\int_0^{\frac{\pi}{2}}\cos^3(\theta)\sin(\theta)d\theta\\ &=\frac{\pi}{2} \end{align}$$

  现在进行重要性采样的集成。$p(\omega)=\frac{1}{2\pi}$，所以我们取$f()/p()=\cos^3(\theta)/\frac{1}{2\pi}$的和的平均值，下面的代码可以测试这一点，并基于蒙特卡洛程序计算上面的积分结果：

#include "rtweekend.h"

#include <iostream>
#include <iomanip>

double f(double r2) {
    // auto x = std::cos(2*pi*r1) * 2 * std::sqrt(r2*(1-r2));
    // auto y = std::sin(2*pi*r1) * 2 * std::sqrt(r2*(1-r2));
    auto z = 1 - r2;
    double cos_theta = z;
    return cos_theta*cos_theta*cos_theta;
}

double pdf() {
    return 1.0 / (2.0*pi);
}

int main() {
    int N = 1000000;

    auto sum = 0.0;
    for (int i = 0; i < N; i++) {
        auto r2 = random_double();
        sum += f(r2) / pdf();
    }

    std::cout << std::fixed << std::setprecision(12);
    std::cout << "PI/2 = " << pi / 2.0 << '\n';
    std::cout << "Estimate = " << sum / N << '\n';
}

7.3. 对半球进行余弦采样

  现在，我们继续尝试求解半球面上的余弦立方，但我们将更改PDF为$p(\omega) = f(\theta) = \cos(\theta)/\pi$，以生成满足该分部的方向。（译者注：这刚好是 Lanbertian的散射 PDF）

$$\begin{align} r_2 &= \int_0^\theta b(\theta')d\theta'\\ &=\int_0^{\theta}2\pi f(\theta')\sin(\theta')d\theta'\\ &=\int_0^{\theta}2\pi \frac{\cos(\theta')}{\pi}\sin(\theta')d\theta'\\ &=1-\cos^2(\theta) \end{align}$$

  可得：

$$\cos(\theta)=\sqrt{1-r_2}$$

  

  通过以下的化简，我们可以在特定情况下节省一点代数运算：

$$z=\cos(\theta)=\sqrt{1-r_2}\\ x = \cos(\phi)\sin(\theta)=\cos(2\pi r_1)\sqrt{1-z^2}=\cos(2\pi r_1)\sqrt{r_2}\\ y = \sin(\phi)\sin(\theta)=\sin(2\pi r_1)\sqrt{1-z^2}=\sin(2\pi r_1)\sqrt{r_2}$$

  下面的函数就是生成服从该PDD定义的分布的随机单位向量：

inline vec3 random_cosine_direction() {
    auto r1 = random_double();
    auto r2 = random_double();

    auto phi = 2*pi*r1;
    auto x = std::cos(phi) * std::sqrt(r2);
    auto y = std::sin(phi) * std::sqrt(r2);
    auto z = std::sqrt(1-r2);

    return vec3(x, y, z);
}

#include "rtweekend.h"

#include <iostream>
#include <iomanip>

double f(const vec3& d) {
    auto cos_theta = d.z();
    return cos_theta*cos_theta*cos_theta;
}

double pdf(const vec3& d) {
    return d.z() / pi;
}

int main() {
    int N = 1000000;

    auto sum = 0.0;
    for (int i = 0; i < N; i++) {
        vec3 d = random_cosine_direction();
        sum += f(d) / pdf(d);
    }

    std::cout << std::fixed << std::setprecision(12);
    std::cout << "PI/2 = " << pi / 2.0 << '\n';
    std::cout << "Estimate = " << sum / N << '\n';
}

  我们以后可以在需要的时候生成其他分布的方向。random_cosine_direction()函数随机生成按$\cos(\theta)$加权的方向，其中，$\theta$是相对于$z$轴的角度。

8. 正交基

  在上一章中，我们实现了生成相对于 $z$ 轴的随机方向的方法。如果我们想要生成与表面解耦的反射光线，我们需要让该方法更具一般性，因为并非所有法线都与 $z$ 轴完全对齐。所以在本章红，我们要将该方法推广到一般，让它能够支持任意表面的法向量。

8.1. 相对坐标系

  正交基是指在空间中三条相互正交的单位向量。它是坐标系中严格定义子空间。笛卡尔坐标系中 $xyz$ 轴就是正交基的一个例子。我们所有的渲染图像都是场景中物体的相对位置和旋转投影到摄像机投影平面上的结果。相机和物体必须使用相同的坐标系表示，使得投影到图像平面上是逻辑正确的，否则相机无法正确渲染物体。必须在对象空间中重新定义相机，或者必须在相机空间中重新定义对象。只要在同一个坐标系中描述相机和场景，一切都很好。正交基定义距离和方向在空间中的表示方式，但仅靠正交基是不够的。物体和相机需要通过它们从共同的原点的位移来描述，例如场景的原点O。它代表宇宙的中心，所有物体都要相对它进行平移。

  假设我们有一个原点$O$和笛卡尔坐标系中的单位向量$x,y,z$。当我们提到坐标$(3,-2,7)$时，实际上是：

$$Location\space is \space O +3x-2y+7z$$

  如果我们想用原点$O′$和基向量$u$、$v$和$w$在另一个坐标系中测量坐标，我们只需找到系数$(u,v,w)$，得到下面的表示：

$$Location\space is \space O' + uU + vV + wW$$

8.2. 生成正交基

  如果你参加图形学入门课程，将花费大量时间在坐标系和$4\times4$ 坐标变换矩阵上。注意，这真的很重要！但是，这本书不介绍它，没有它我们就凑合着用。我们确实需要生成具有相对于表面法向量$n$的固定分布的随机方向。我们不需要原点，因为方向是相对的，没有特定的原点。首先，我们需要两个余切向量，每个向量都垂直于n，它们也互相垂直。

  一些3D物体模型将为每个顶点提供一个或多个余切向量。如果我们的模型只有一个余切向量，那么生成正交基（ONB）的过程就是一个必要的过程。假设我们有任意长度非零且与 $n$ 不平行的向量 $a$。我们可以利用叉积的性质，使用 $n\times a$ 获得垂直于 $n$ 和 $a$ 的向量 $s$ 和 $t$：

$$s=unit\_vector(n\times a)\\ t = n \times s$$

  看起来一切都很美好，可问题是，当我们加载模型时，我们可能无法给出向量 $a$，并且我们的程序还没有生成它的方法。如果我们强行选择一个任意的 $a$ 作为初始向量，我们可能会得到一个与 $n$ 平行的 $a$。所以普遍的做法是选取任意的 $a$ ，并检查它与$n$是否平行（假设向量都是单位向量，长度为1），如果是，则选取另一个轴：

if (std::fabs(n.x()) > 0.9)
    a = vec3(0, 1, 0)
else
    a = vec3(1, 0, 0)

  然后就可以通过叉积来获得 $s$ 和 $t$ ：

vec3 s = unit_vector(cross(n, a));
vec3 t = cross(n, s);

  注意，我们不需要对向量 $t$ 进行归一化。因为 $n$ 和 $s$ 都是单位向量，他们的叉积 $t$ 也一定是单位向量。一旦我们有了由$s$，$t$，$n$ 组成的正交基，并且有相对于 $z$ 轴的随机坐标 $(x,y,z)$，我们就可以得到相对于 $n$ 的向量：

$$random\space vector = xs +yt +zn$$

  如果你还记得，我们使用相似的数学方法来生成以相机位置为起点的射线。你可以将其视为对相机坐标系的表示。

8.3. 正交基类

  我们应该为正交基创建一个类，还是创建通用程序函数就足够了？我不确定，但让我们创建一个类，因为它不会比实现通用函数更复杂：

#ifndef ONB_H
#define ONB_H

class onb {
  public:
    onb(const vec3& n) {
        axis[2] = unit_vector(n);
        vec3 a = (std::fabs(axis[2].x()) > 0.9) ? vec3(0,1,0) : vec3(1,0,0);
        axis[1] = unit_vector(cross(axis[2], a));
        axis[0] = cross(axis[2], axis[1]);
    }

    const vec3& u() const { return axis[0]; }
    const vec3& v() const { return axis[1]; }
    const vec3& w() const { return axis[2]; }

    vec3 transform(const vec3& v) const {
        // Transform from basis coordinates to local space.
        return (v[0] * axis[0]) + (v[1] * axis[1]) + (v[2] * axis[2]);
    }

  private:
    vec3 axis[3];
};


#endif

  我们可以重写Lanbertian材质来使用该类，实现如下：

#include "hittable.h"
#include "onb.h"
#include "texture.h"

class material {
  public:
    ...

    virtual bool scatter(
        const ray& r_in, const hit_record& rec, color& attenuation, ray& scattered, double& pdf
    ) const {
        return false;
    }

    ...
};

class lambertian : public material {
  public:
    ...

    bool scatter(
        const ray& r_in, const hit_record& rec, color& attenuation, ray& scattered, double& pdf
    ) const override {
        onb uvw(rec.normal);
        auto scatter_direction = uvw.transform(random_cosine_direction());

        scattered = ray(rec.p, unit_vector(scatter_direction), r_in.time());
        attenuation = tex->value(rec.u, rec.v, rec.p);
        pdf = dot(uvw.w(), scattered.direction()) / pi;
        return true;
    }

    ...
};

class metal : public material {
  public:
    ...

    bool scatter(
        const ray& r_in, const hit_record& rec, color& attenuation, ray& scattered, double& pdf
    ) const override {
        ...
    }
};

class dielectric : public material {
  public:
    ...

    bool scatter(
        const ray& r_in, const hit_record& rec, color& attenuation, ray& scattered, double& pdf
    ) const override {
        ...
    }
};

class diffuse_light : public material {
    ...
};

class isotropic : public material {
  public:
    ...

    bool scatter(
        const ray& r_in, const hit_record& rec, color& attenuation, ray& scattered, double& pdf
    ) const override {
        ...
    }
};

  在下面的代码中，我们将更改也应用到camera类中：

class camera {
  ...
  private:
    ...

    color ray_color(const ray& r, int depth, const hittable& world) const {
        ...

        ray scattered;
        color attenuation;
        double pdf_value;
        color color_from_emission = rec.mat->emitted(rec.u, rec.v, rec.p);

        if (!rec.mat->scatter(r, rec, attenuation, scattered, pdf_value))
            return color_from_emission;

        double scattering_pdf = rec.mat->scattering_pdf(r, rec, scattered);
        pdf_value = scattering_pdf;

        ...
    }

    ...
};

  渲染结果如下：

  让我们消除一些噪点。

  然而在此之前，让我们先更新isotropic材质：

class isotropic : public material {
  public:
    isotropic(const color& albedo) : tex(make_shared<solid_color>(albedo)) {}
    isotropic(shared_ptr<texture> tex) : tex(tex) {}

    bool scatter(
        const ray& r_in, const hit_record& rec, color& attenuation, ray& scattered, double& pdf
    ) const override {
        scattered = ray(rec.p, random_unit_vector(), r_in.time());
        attenuation = tex->value(rec.u, rec.v, rec.p);
        pdf = 1 / (4 * pi);
        return true;
    }

    double scattering_pdf(const ray& r_in, const hit_record& rec, const ray& scattered)
    const override {
        return 1 / (4 * pi);
    }

  private:
    shared_ptr<texture> tex;
};

9. 采样光源方向

  在所有方向上均匀采样的问题在于，在任意或不重要的方向上，灯光被采样的概率应该降低。我们可以使用阴影射线来求解任何给定点的直接光照。相反，我将使用朝光源发射更多射线的PDF。然后，我们可以回过头来更改该PDF，以向我们想要的任何方向发送更多光线。

  朝光源获取一个随机的方向非常简单。只需要在光源上随机选择一个点并在该方向上发射射线即可。但是，我们还需要知道PDF，$p(\omega)$，确保我们没有让渲染结果偏离正确方向。但是，它是什么呢？

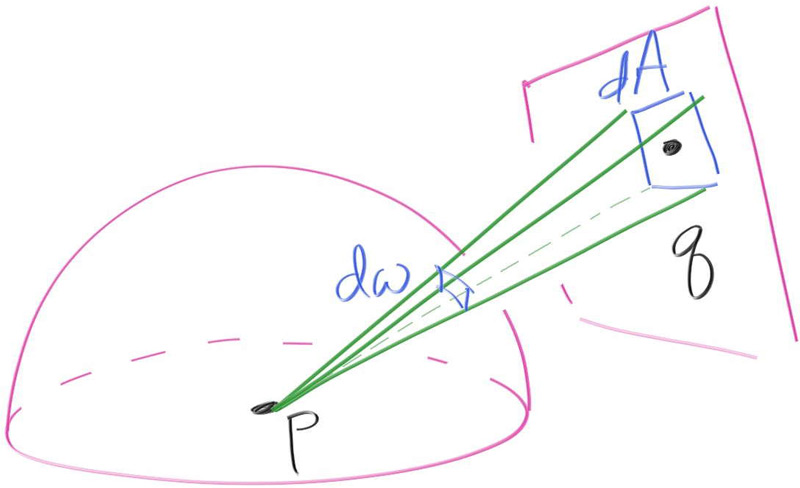
9.1. 获取光源PDF

  对于面积为$A$的面光源，如果我们在它上面均匀采样，则PDF是$\frac{1}{A}$。而整个表面投影到单位球上的面积是多少呢？幸运的是，这有一个简单的对应，如下图所示：

  如果我们看向光源中的一个小区域$dA$，射线碰到它的概率是$p_q(q)\cdot dA$。在球体表面，采样到该小区域$d\omega$的概率是$p(\omega)\cdot d\omega$。在$d\omega$和$dA$之间，存在一定的几何关系：

$$d\omega = \frac{dA \cdot \cos(\theta)}{distance^2(p,q)}$$

  由于采样$d\omega$和$dA$的概率必须一样，所以：

$$p(\omega)\cdot dw = p_q(q)\cdot dA\\ p(\omega)\cdot \frac{dA\cdot \cos(\theta)}{distance^2(p,q)}=p_q(q)\cdot dA$$

  已知在光源表面上随机采样的PDF是$\frac{1}{A}$:

$$p_q(q)=\frac{1}{A}\\ p(\omega)\cdot\frac{dA\cdot\cos(\theta)}{distance^2(p,q)}=\frac{dA}{A}$$

  化简可得：

$$p(\omega)=\frac{distance^2(p,q)}{\cos(\theta)\cdot A}$$

9.2. 采样光源

  我们可以强制让ray_color()函数采样光源，用以检查我们数学原理和概念的编码实现是否正确：

class camera {
  ...
  private:
    ...

    color ray_color(const ray& r, int depth, const hittable& world) const {
        // If we've exceeded the ray bounce limit, no more light is gathered.
        if (depth <= 0)
            return color(0,0,0);

        hit_record rec;

        // If the ray hits nothing, return the background color.
        if (!world.hit(r, interval(0.001, infinity), rec))
            return background;

        ray scattered;
        color attenuation;
        double pdf_value;
        color color_from_emission = rec.mat->emitted(rec.u, rec.v, rec.p);

        if (!rec.mat->scatter(r, rec, attenuation, scattered, pdf_value))
            return color_from_emission;

        auto on_light = point3(random_double(213,343), 554, random_double(227,332));
        auto to_light = on_light - rec.p;
        auto distance_squared = to_light.length_squared();
        to_light = unit_vector(to_light);

        if (dot(to_light, rec.normal) < 0)
            return color_from_emission;

        double light_area = (343-213)*(332-227);
        auto light_cosine = std::fabs(to_light.y());
        if (light_cosine < 0.000001)
            return color_from_emission;

        pdf_value = distance_squared / (light_cosine * light_area);
        scattered = ray(rec.p, to_light, r.time());

        double scattering_pdf = rec.mat->scattering_pdf(r, rec, scattered);

        color color_from_scatter =
            (attenuation * scattering_pdf * ray_color(scattered, depth-1, world)) / pdf_value;

        return color_from_emission + color_from_scatter;
    }
};

  我们把场景的samples_per_pixel设置为10来测试这些代码：

int main() {
    ...
    cam.aspect_ratio      = 1.0;
    cam.image_width       = 600;
    cam.samples_per_pixel = 10;
    cam.max_depth         = 50;
    cam.background        = color(0,0,0);
    ...
}

  渲染结果如下：

  这与我们对仅对光源采样的期望结果差不多，因此看起来正确了。

9.3. 切换到单向光

  在光源周围的噪点是由于光源是双面的，并且这里在光源天花板之间有一个狭小的空间。我们可能希望光线只是往下发射。我们可以让hitable_emitted()函数接受更多额外的参数 ：

class material {
  public:
    ...

    virtual color emitted(
        const ray& r_in, const hit_record& rec, double u, double v, const point3& p
    ) const {
        return color(0,0,0);
    }
    ...
};

class diffuse_light : public material {
  public:
    ...

    color emitted(const ray& r_in, const hit_record& rec, double u, double v, const point3& p)
    const override {
        if (!rec.front_face)
            return color(0,0,0);
        return tex->value(u, v, p);
    }

    ...
};

class camera {
  ...
  private:
    color ray_color(const ray& r, int depth, const hittable& world) const {
        ...

        color color_from_emission = rec.mat->emitted(r, rec, rec.u, rec.v, rec.p);

        ...
    }
};

  渲染结果如下：

10. 混合密度

  我们使用了与$\cos(\theta)$ 相关的PDF和与光采样相关的PDF。我们想要一个包含这些所有内容的PDF。

10.1. PDF类

  我们已经在相当多的代码中使用了PDF。我认为现在是弄清楚我们如何标准化PDF使用的好时机。我们已经知道我们将有一个用于表面的PDF和一个用于光源的PDF，因此让我们创建一个pdf基类。到目前为止，我们有一个pdf() 函数，它接受一个方向并返回该方向的PDF分布值。到目前为止，这个值一直是$\frac{1}{4\pi}$、$\frac{1}{2\pi}$和$\frac{\cos(\theta)}{\pi}$中的一个。在我们的几个例子中，我们生成了不同分布的随机方向。我们在第六章中对此进行了相当多的介绍。一般来说，如果我们知道随机方向的分布，我们应该使用具有相同分布的PDF。这会使计算结果收敛速度更快。考虑到这一点，我们将创建一个pdf类，该类负责生成随机方向并确定PDF的值。

  综上所述，任何pdf类都应该能够支持：

1. 返回由内部 PDF 分布加权的随机方向
2. 返回该方向上的相应PDF的值。

  $pSurface$ 和 $pLight$ 在背后实现的细节各不相同，而这可以通过类的继承来轻松实现。抽象类中的内容从来都不是显而易见的，所以我的方法是贪婪并希望最小的接口有效，对于pdf这意味着：

#ifndef PDF_H
#define PDF_H

#include "onb.h"


class pdf {
  public:
    virtual ~pdf() {}

    virtual double value(const vec3& direction) const = 0;
    virtual vec3 generate() const = 0;
};

#endif

  我们将看看是否需要通过填充子类来向pdf添加任何其他内容。首先，我们将创建单位球体上均匀采样的PDF：

class sphere_pdf : public pdf {
  public:
    sphere_pdf() {}

    double value(const vec3& direction) const override {
        return 1/ (4 * pi);
    }

    vec3 generate() const override {
        return random_unit_vector();
    }
};

  随后，让我们实现余弦PDF：

class cosine_pdf : public pdf {
  public:
    cosine_pdf(const vec3& w) : uvw(w) {}

    double value(const vec3& direction) const override {
        auto cosine_theta = dot(unit_vector(direction), uvw.w());
        return std::fmax(0, cosine_theta/pi);
    }

    vec3 generate() const override {
        return uvw.transform(random_cosine_direction());
    }

  private:
    onb uvw;
};

  我们可以在ray_color()函数中尝试使用余弦密度函数：

#include "hittable.h"
#include "pdf.h"
#include "material.h"

class camera {
  ...
  private:
    ...
    color ray_color(const ray& r, int depth, const hittable& world) const {
        // If we've exceeded the ray bounce limit, no more light is gathered.
        if (depth <= 0)
            return color(0,0,0);

        hit_record rec;

        // If the ray hits nothing, return the background color.
        if (!world.hit(r, interval(0.001, infinity), rec))
            return background;

        ray scattered;
        color attenuation;
        double pdf_value;
        color color_from_emission = rec.mat->emitted(r, rec, rec.u, rec.v, rec.p);

        if (!rec.mat->scatter(r, rec, attenuation, scattered, pdf_value))
            return color_from_emission;

        cosine_pdf surface_pdf(rec.normal);
        scattered = ray(rec.p, surface_pdf.generate(), r.time());
        pdf_value = surface_pdf.value(scattered.direction());

        double scattering_pdf = rec.mat->scattering_pdf(r, rec, scattered);

        color color_from_scatter =
            (attenuation * scattering_pdf * ray_color(scattered, depth-1, world)) / pdf_value;

        return color_from_emission + color_from_scatter;
    }
};

  把samples_per_pixel重新设置为1000：

int main() {
    ...
    cam.aspect_ratio      = 1.0;
    cam.image_width       = 600;
    cam.samples_per_pixel = 1000;
    cam.max_depth         = 50;
    cam.background        = color(0,0,0);
    ...
}

  这会产生精准匹配的结果，到目前为止，我们只是把一些计算移到了cosine_pdf类中：

10.2. 朝向Hittable的采样方向

  现在我们可以尝试对 hittable 进行采样，像对光源那样：

#include "hittable_list.h"
#include "onb.h"

...

class hittable_pdf : public pdf {
  public:
    hittable_pdf(const hittable& objects, const point3& origin)
      : objects(objects), origin(origin)
    {}

    double value(const vec3& direction) const override {
        return objects.pdf_value(origin, direction);
    }

    vec3 generate() const override {
        return objects.random(origin);
    }

  private:
    const hittable& objects;
    point3 origin;
};

  如果我们想对光线进行采样，我们将需要 hittable 来回答一些它还没有接口的查询。上面的代码假设 hittable 类中存在两个尚未实现的函数：pdf_value() 和 random()。我们需要添加这些函数才能编译程序。我们可以遍历所有 hittable 子类并添加这些函数，但这会很麻烦，所以我们只向 hittable 基类添加两个简单的函数。这打破了我们以前纯粹的抽象实现，但它节省了工作。如果你想要一个纯粹抽象的 hittable 接口类，可以随意将这些函数重写到子类中。

class hittable {
  public:
    virtual ~hittable() = default;

    virtual bool hit(const ray& r, interval ray_t, hit_record& rec) const = 0;

    virtual aabb bounding_box() const = 0;

    virtual double pdf_value(const point3& origin, const vec3& direction) const {
        return 0.0;
    }

    virtual vec3 random(const point3& origin) const {
        return vec3(1,0,0);
    }
};

  然后，我们修改quad来实现这些函数：

class quad : public hittable {
  public:
    quad(const point3& Q, const vec3& u, const vec3& v, shared_ptr<material> mat)
      : Q(Q), u(u), v(v), mat(mat)
    {
        auto n = cross(u, v);
        normal = unit_vector(n);
        D = dot(normal, Q);
        w = n / dot(n,n);

        area = n.length();

        set_bounding_box();
    }

    ...

    double pdf_value(const point3& origin, const vec3& direction) const override {
        hit_record rec;
        if (!this->hit(ray(origin, direction), interval(0.001, infinity), rec))
            return 0;

        auto distance_squared = rec.t * rec.t * direction.length_squared();
        auto cosine = std::fabs(dot(direction, rec.normal) / direction.length());

        return distance_squared / (cosine * area);
    }

    vec3 random(const point3& origin) const override {
        auto p = Q + (random_double() * u) + (random_double() * v);
        return p - origin;
    }

  private:
    point3 Q;
    vec3 u, v;
    vec3 w;
    shared_ptr<material> mat;
    aabb bbox;
    vec3 normal;
    double D;
    double area;
};

  我们只需要增加pdf_value()和random()到quad中，因为我们使用这些内容来对光源进行重要性采样，而在我们场景中只有一盏面光源，用quad表示。如果你想要其他几何光源，或者想要使用其他物体的PDF，你需要实现上述函数到相应的类中。

  给相机的render()函数增加lights的参数：

class camera {
  public:
    ...

    void render(const hittable& world, const hittable& lights) {
        initialize();

        std::cout << "P3\n" << image_width << ' ' << image_height << "\n255\n";

        for (int j = 0; j < image_height; j++) {
            std::clog << "\rScanlines remaining: " << (image_height - j) << ' ' << std::flush;
            for (int i = 0; i < image_width; i++) {
                color pixel_color(0,0,0);
                for (int s_j = 0; s_j < sqrt_spp; s_j++) {
                    for (int s_i = 0; s_i < sqrt_spp; s_i++) {
                        ray r = get_ray(i, j, s_i, s_j);
                        pixel_color += ray_color(r, max_depth, world, lights);
                    }
                }
                write_color(std::cout, pixel_samples_scale * pixel_color);
            }
        }

        std::clog << "\rDone.                 \n";
    }

    ...
  private:
    ...

    color ray_color(const ray& r, int depth, const hittable& world, const hittable& lights)
    const {
        ...

        ray scattered;
        color attenuation;
        double pdf_value;
        color color_from_emission = rec.mat->emitted(r, rec, rec.u, rec.v, rec.p);

        if (!rec.mat->scatter(r, rec, attenuation, scattered, pdf_value))
            return color_from_emission;

        hittable_pdf light_pdf(lights, rec.p);
        scattered = ray(rec.p, light_pdf.generate(), r.time());
        pdf_value = light_pdf.value(scattered.direction());

        double scattering_pdf = rec.mat->scattering_pdf(r, rec, scattered);

        color sample_color = ray_color(scattered, depth-1, world, lights);
        color color_from_scatter = (attenuation * scattering_pdf * sample_color) / pdf_value;

        return color_from_emission + color_from_scatter;
    }
};

  在天花板中间增加光源：

int main() {
    ...

    // Box 2
    shared_ptr<hittable> box2 = box(point3(0,0,0), point3(165,165,165), white);
    box2 = make_shared<rotate_y>(box2, -18);
    box2 = make_shared<translate>(box2, vec3(130,0,65));
    world.add(box2);

    // Light Sources
    auto empty_material = shared_ptr<material>();
    quad lights(point3(343,554,332), vec3(-130,0,0), vec3(0,0,-105), empty_material);

    camera cam;

    cam.aspect_ratio      = 1.0;
    cam.image_width       = 600;
    cam.samples_per_pixel = 10;
    cam.max_depth         = 50;
    cam.background        = color(0,0,0);

    ...

    cam.render(world, lights);
}

  设置samples_per_pixel为10，渲染结果如下：

  译者注：这里增加的光源使用的是空材质，它不会为打到它身上的光线贡献颜色。在程序中，它只是一个占位，表示光源的形状和位置，只贡献 PDF 和散射方向。

10.3. 混合PDF类

  正如前面尝试重要性采样这一章中提到的，我们可以创建PDF的线性组合来获得混合概率密度函数。PDF的加权平均仍然是PDF。只要权值是正值且每一项权值的和为1，这样我们就有了一个新的PDF。

$$pMixture()=\omega_0p_0()+\omega_1p_1() + ... + \omega_{n-1}p_{n-1}()\\ 1 = \omega_0 + \omega_1 + ... \omega_{n-1}$$

  例如，我们可以对下面两个PDF值取平均。

$$pMixture(\omega_o)=\frac{1}{2}pSurface(\omega_o) + \frac{1}{2}pLight(\omega_o)$$

  我们如何修改我们的代码来支持这一点呢？有一个非常重要的细节使这并不像人们想象的那么容易。生成混合PDF的随机方向很简单：

if (random_double() < 0.5)
    pick direction according to pSurface
else
    pick direction according to pLight

  但是求解$pMixture$的PDF值有一些不同。我们不能像下面这样：

if (direction is from pSurface)
    get PDF value of pSurface
else
    get PDF value of pLight

  首先，弄清楚随机方向来自哪个PDF可能并非易事。我们没有任何机制让generate() 告诉value()原来的random_double() 是什么，所以我们不能简单地说出随机方向来自哪个PDF。如果我们认为上述内容是正确的，我们将不得不回溯求解以计算方向所属的PDF。老实说，这听起来像是一场噩梦，但幸运的是我们不需要这样做。两个PDF都可能生成了一些方向。例如，朝向光线的方向可能由 $pLight$ 或 $pSurface$ 生成。对于我们来说，求解随机方向的 $pSurface$ 和 $pLight$ 的PDF值就足够了，然后取PDF混合权重来求解该方向的总PDF值。混合密度类实际上非常简单：

class mixture_pdf : public pdf {
  public:
    mixture_pdf(shared_ptr<pdf> p0, shared_ptr<pdf> p1) {
        p[0] = p0;
        p[1] = p1;
    }

    double value(const vec3& direction) const override {
        return 0.5 * p[0]->value(direction) + 0.5 *p[1]->value(direction);
    }

    vec3 generate() const override {
        if (random_double() < 0.5)
            return p[0]->generate();
        else
            return p[1]->generate();
    }

  private:
    shared_ptr<pdf> p[2];
};

  现在我们想做余弦采样和光采样的混合密度。我们可以将其代入ray_color()：

class camera {
  ...
  private:
    ...

    color ray_color(const ray& r, int depth, const hittable& world, const hittable& lights)
    const {
        ...

        if (!rec.mat->scatter(r, rec, attenuation, scattered, pdf_value))
            return color_from_emission;

        auto p0 = make_shared<hittable_pdf>(lights, rec.p);
        auto p1 = make_shared<cosine_pdf>(rec.normal);
        mixture_pdf mixed_pdf(p0, p1);

        scattered = ray(rec.p, mixed_pdf.generate(), r.time());
        pdf_value = mixed_pdf.value(scattered.direction());

        double scattering_pdf = rec.mat->scattering_pdf(r, rec, scattered);

        color sample_color = ray_color(scattered, depth-1, world, lights);
        color color_from_scatter = (attenuation * scattering_pdf * sample_color) / pdf_value;

        return color_from_emission + color_from_scatter;
    }

  更新main.cc并设置samples_per_pixel为1000，渲染结果如下：

11. 一些架构决策

  本章我们不会编写任何代码。我们正处于十字路口，需要做出一些架构决策。

  混合密度的方法是传统的阴影射线的替代方法。这些光线用于检查从交点到给定光源的畅通无阻的路径。在点和给定光源之间与对象相交的光线表示交点位于该特定光源的阴影中。我个人更喜欢混合密度的方法，因为除了灯光之外，你还可以对窗户或门下明亮的裂缝或任何你认为可能明亮或重要的东西进行采样。但你仍然会在大多数专业路径追踪渲染器中看到阴影射线。通常，它们将具有预定义数量的阴影射线（例如 1、4、8、16），在渲染过程中，在路径追踪光线相交的每个位置，它们会将这些阴影射线发送到场景中的随机光源，以确定交点是否由该随机光源照亮。交点将由该光源照亮，或完全处于阴影中，其中更多的阴影光线会导致更精确的照明。在所有阴影射线终止后（在灯光或遮挡曲面处），初始路径跟踪光线将继续，并在下一个交点处发送更多阴影射线。你无法说明阴影射线什么是重要的，只能告诉它们什么是自发光的，因此阴影射线最适合没有过于复杂的光子分布的简单场景。也就是说，阴影射线在它们交到的第一个物体时终止，并且不会四处反弹，因此一条阴影射线比一条路径追踪的射线消耗更小，这就是为什么你通常会看到比路径追踪光线多得多的阴影射线（例如 1、4、8、16）。在更受限制的场景中，你可以选择阴影射线而不是混合密度。这是个人的设计偏好。对于粗略的结果，阴影射线往往比混合物密度性能更优，并且在实时程序中，也越来越普遍地被使用。

  在我们代码中，还有其他问题。

  PDF的构造是硬编码在ray_color()函数里的。我们应该把它清理掉。

  我们不小心破坏了镜面反射光线（玻璃和金属），因此它们目前还未实现新增的接口。如果我们只是将他们的散射函数设为增量函数，数学将继续计算，但这会导致各种浮点数的问题。我们可以将镜面反射作为跳过f()/p()的特例，或者我们可以将表面粗糙度设置为一个非常小但非零的值，并获得看起来非常平滑且不会产生NaN的渲染结果。我对使用哪种方法没有意见（我都尝试过，它们都有各自的优点），但无论如何我们都会实现平滑的金属和玻璃代码，因此我们将添加完美的镜面反射表面，这些表面只是跳过显式的 f()/p() 计算。

  我们还缺乏真实背景函数的基础设施，以便于我们可以添加环境映射或更有趣的背景。某些环境贴图是HDR（RGB分量是标准化浮点数，而不是0–255字节）。我们的输出一直是HDR，只不过我们一直在截断它。

  最后，我们的渲染器是RGB的。一个更基于物理的——就像汽车制造商可能使用的那样——可能需要使用光谱颜色，甚至可能需要利用光的偏振。对于电影制作中使用的渲染器，大多数工作室仍然使用RGB。你也可以制作同时具有两种模式的混合渲染器，不过这会更难。我现在打算坚持使用RGB，我会在本书的结尾谈到这一点。

We also lack a real background function infrastructure in case we want to add an environment map or a more interesting functional background. Some environment maps are HDR (the RGB components are normalized floats rather than 0–255 bytes). Our output has been HDR all along; we’ve just been truncating it.

12. 整理PDF的管理类

  到目前为止，我将两种PDF硬编码在ray_color()函数中：

1. p0()与光源的形状相关
2. p1()与法线和物体表面的类型有关

  我们可以把光源（或者任何我们想采样的hittable）信息传给ray_color()函数，并且，我们可以通过material的函数来获得PDF（我们必须增加一些实现来达到这个目的）。我们还需要知道散射光线是否为镜面高光，为此我们可以通过hit()函数或material类来实现。

12.1 漫反射表面 vs 镜面

  我们想要考虑的一件事情是材质表面有部分是理想的镜面反射（抛光）和部分漫反射（木材），例如清漆木材。一些渲染器让材质生成两种射线：一个镜面高光，另一个是漫反射。我不喜欢分支，所以我宁愿让材质随机决定它是漫反射还是镜面反射。这种方法的缺点是，当我们计算PDF值时需要小心，并且 ray_color() 需要知道这条射线是漫反射的还是镜面反射的。幸运的是，我们已经决定只在它是漫反射时才调用pdf_value()，这样我们就可以隐式地处理它。

  我们可以重新设计material，并将所有新参数塞入一个类中，就像我们对 hittable 所做的那样：

#include "hittable.h"
#include "onb.h"
#include "texture.h"

class scatter_record {
  public:
    color attenuation;
    shared_ptr<pdf> pdf_ptr;
    bool skip_pdf;
    ray skip_pdf_ray;
};

class material {
  public:
    ...

    virtual bool scatter(const ray& r_in, const hit_record& rec, scatter_record& srec) const {
        return false;
    }

    ...
};

  lambertian材质变得更精简：

#include "hittable.h"
// #include "onb.h"
#include "pdf.h"
#include "texture.h"

...

class lambertian : public material {
  public:
    lambertian(const color& albedo) : tex(make_shared<solid_color>(albedo)) {}
    lambertian(shared_ptr<texture> tex) : tex(tex) {}

    bool scatter(const ray& r_in, const hit_record& rec, scatter_record& srec) const override {
        srec.attenuation = tex->value(rec.u, rec.v, rec.p);
        srec.pdf_ptr = make_shared<cosine_pdf>(rec.normal);
        srec.skip_pdf = false;
        return true;
    }

    double scattering_pdf(const ray& r_in, const hit_record& rec, const ray& scattered)
    const override {
        auto cos_theta = dot(rec.normal, unit_vector(scattered.direction()));
        return cos_theta < 0 ? 0 : cos_theta/pi;
    }

  private:
    shared_ptr<texture> tex;
};

  isotropic材质也是如此：

class isotropic : public material {
  public:
    isotropic(const color& albedo) : tex(make_shared<solid_color>(albedo)) {}
    isotropic(shared_ptr<texture> tex) : tex(tex) {}

    bool scatter(const ray& r_in, const hit_record& rec, scatter_record& srec) const override {
        srec.attenuation = tex->value(rec.u, rec.v, rec.p);
        srec.pdf_ptr = make_shared<sphere_pdf>();
        srec.skip_pdf = false;
        return true;
    }

    double scattering_pdf(const ray& r_in, const hit_record& rec, const ray& scattered)
    const override {
        return 1 / (4 * pi);
    }

  private:
    shared_ptr<texture> tex;
};

  ray_color()的改动很小：

class camera {
  ...
  private:
    ...

    color ray_color(const ray& r, int depth, const hittable& world, const hittable& lights)
    const {
        // If we've exceeded the ray bounce limit, no more light is gathered.
        if (depth <= 0)
            return color(0,0,0);

        hit_record rec;

        // If the ray hits nothing, return the background color.
        if (!world.hit(r, interval(0.001, infinity), rec))
            return background;

        scatter_record srec;
        color color_from_emission = rec.mat->emitted(r, rec, rec.u, rec.v, rec.p);

        if (!rec.mat->scatter(r, rec, srec))
            return color_from_emission;

        auto light_ptr = make_shared<hittable_pdf>(lights, rec.p);
        mixture_pdf p(light_ptr, srec.pdf_ptr);

        ray scattered = ray(rec.p, p.generate(), r.time());
        auto pdf_value = p.value(scattered.direction());

        double scattering_pdf = rec.mat->scattering_pdf(r, rec, scattered);

        color sample_color = ray_color(scattered, depth-1, world, lights);
        color color_from_scatter =
            (srec.attenuation * scattering_pdf * sample_color) / pdf_value;

        return color_from_emission + color_from_scatter;
    }
};

12.2 处理镜面反射

  我们还没有处理表面的镜面发射，也尚未处理与表面法线冲突的实例。不过，该设计总体上是简洁的，而且都是可以修复的。现在，我准备修复specular。金属和电介质材质很容易就修复了：

class metal : public material {
  public:
    metal(const color& albedo, double fuzz) : albedo(albedo), fuzz(fuzz < 1 ? fuzz : 1) {}

    bool scatter(const ray& r_in, const hit_record& rec, scatter_record& srec) const override {
        vec3 reflected = reflect(r_in.direction(), rec.normal);
        reflected = unit_vector(reflected) + (fuzz * random_unit_vector());

        srec.attenuation = albedo;
        srec.pdf_ptr = nullptr;
        srec.skip_pdf = true;
        srec.skip_pdf_ray = ray(rec.p, reflected, r_in.time());

        return true;
    }

  private:
    color albedo;
    double fuzz;
};

class dielectric : public material {
  public:
    dielectric(double refraction_index) : refraction_index(refraction_index) {}

    bool scatter(const ray& r_in, const hit_record& rec, scatter_record& srec) const override {
        srec.attenuation = color(1.0, 1.0, 1.0);
        srec.pdf_ptr = nullptr;
        srec.skip_pdf = true;
        double ri = rec.front_face ? (1.0/refraction_index) : refraction_index;

        vec3 unit_direction = unit_vector(r_in.direction());
        double cos_theta = std::fmin(dot(-unit_direction, rec.normal), 1.0);
        double sin_theta = std::sqrt(1.0 - cos_theta*cos_theta);

        bool cannot_refract = ri * sin_theta > 1.0;
        vec3 direction;

        if (cannot_refract || reflectance(cos_theta, ri) > random_double())
            direction = reflect(unit_direction, rec.normal);
        else
            direction = refract(unit_direction, rec.normal, ri);

        srec.skip_pdf_ray = ray(rec.p, direction, r_in.time());
        return true;
    }

  ...
};

  请注意，如果模糊度为非零，则此表面并不是真正理想的镜面反射，但隐式采样的工作方式与以前一样。在处理镜面反射时，我们在相关材质中跳过了PDF的工作。

  ray_color()只需要增加一些新的判断来生成隐式采样的光线：

class camera {
  ...
  private:
    ...
    color ray_color(const ray& r, int depth, const hittable& world, const hittable& lights)
    const {
        ...

        if (!rec.mat->scatter(r, rec, srec))
            return color_from_emission;

        if (srec.skip_pdf) {
            return srec.attenuation * ray_color(srec.skip_pdf_ray, depth-1, world, lights);
        }

        auto light_ptr = make_shared<hittable_pdf>(lights, rec.p);
        mixture_pdf p(light_ptr, srec.pdf_ptr);

        ...
    }
};

  我们将场景中一个方块的材质改成metal来检验我们的修改。我们还会把其中方块换成玻璃材质的物体，不过这是下一小节的事情。玻璃物体要渲染好，比较困难，所以我们想给它定义PDF，在此之前，先把本小节的内容完成：

int main() {
    ...
    // Light
    world.add(make_shared<quad>(point3(213,554,227), vec3(130,0,0), vec3(0,0,105), light));

    // Box 1
    shared_ptr<material> aluminum = make_shared<metal>(color(0.8, 0.85, 0.88), 0.0);
    shared_ptr<hittable> box1 = box(point3(0,0,0), point3(165,330,165), aluminum);
    box1 = make_shared<rotate_y>(box1, 15);
    box1 = make_shared<translate>(box1, vec3(265,0,295));
    world.add(box1);

    // Box 2
    shared_ptr<hittable> box2 = box(point3(0,0,0), point3(165,165,165), white);
    box2 = make_shared<rotate_y>(box2, -18);
    box2 = make_shared<translate>(box2, vec3(130,0,65));
    world.add(box2);

    // Light Sources
    auto empty_material = shared_ptr<material>();
    quad lights(point3(343,554,332), vec3(-130,0,0), vec3(0,0,-105), empty_material);

    ...
}

  渲染结果在天花板上有噪点，因为朝向长方体的方向没有以更高的密度进行采样。

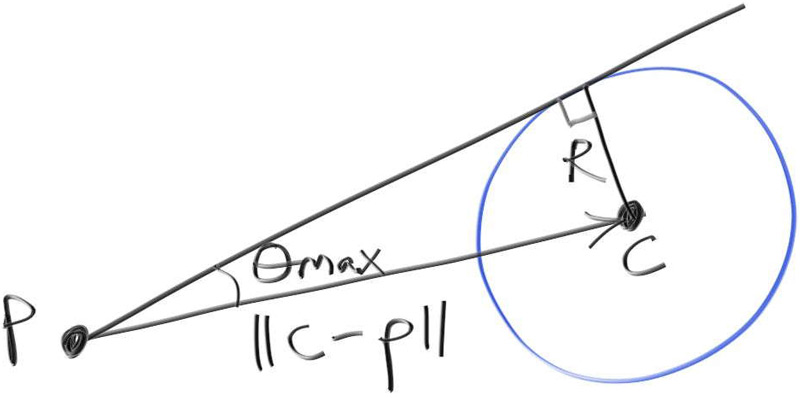
12.3. 采样球形物体

  天花板的噪点可以通过为金属方块定义PDF来减小。如果我们想把它做成玻璃材质，也需要另外为玻璃材质定义PDF。但是为方块制作PDF是一项相当繁重的工作，而且不是很有趣，所以让我们为玻璃球定义一个PDF。它更快，且让渲染更有趣。我们需要弄清楚如何对球体进行采样以确定适当的PDF分布。如果我们从球体的外部的一点采样它，我们不能仅仅只是从它的表面上随机选择一个点。如果这么做了，我们通常会从球体面向该点较远的一侧选取随机点，这些点会被较近一侧的表面挡住。我们需要一种均匀的采样方法，该方法从球体上对外侧一点可见的那一面进行均匀采样。当我们从球体外的一点均匀地对球体的立体角进行采样时，我们实际上只是对圆锥体进行均匀采样。该圆锥体的中心轴从射线起点开始，指向球心，圆锥体的侧面与球体相切，如下图所示。假设代码具有theta_max。重温生成随机方向这一章，方向与轴成 $\theta$ 角的方向的采样，有如下公式：

$$r_2 = \int_0^\theta 2\pi f(\theta')\sin(\theta')d\theta'$$

  这里$f(\theta’)$是一个未计算的常数$C$，有：

$$r_2=\int_0^{\theta}2\pi C\sin(\theta')d\theta'$$

  如果我们通过微积分求解，可得：

$$r_2 = 2\pi\cdot C(1-\cos(\theta))$$

  则：

$$\cos(\theta)=1-\frac{r_2}{2\pi\cdot C}$$

  该分布有一个约束，即随机方向与轴的夹角，必须小于$\theta_{max}$。这意味着该函数在$[0, \theta_{max}]$上的积分为1，即上式中的$r_2$为1。我们便可以求解$C$:

$$r_2 = 2\pi\cdot C \cdot(1-\cos(\theta))\\ 1 = 2\pi\cdot C \cdot(1-\cos(\theta_{max}))\\ C = \frac{1}{2\pi\cdot(1-\cos(\theta_{max}))}$$

  这就给出了一个$\theta$，$\theta_{max}$和$r_2$之间的关系式：

$$\cos(\theta)=1 + r_2\cdot(\cos(\theta_{max})-1)$$

  对$\phi$的采样和之前一样：

$$z = \cos(\theta) = 1+r_2\cdot(\cos(\theta_{max})-1)\\ x = \cos(\phi)\cdot\sin(\theta)=\cos(2\pi\cdot r_1)\cdot \sqrt{1-z^2}\\ y = \sin(\phi)\cdot\sin(\theta)=\sin(2\pi\cdot r_1)\cdot \sqrt{1-z^2}$$

  那么还剩下一个疑问：$\theta_{max}$是什么呢？

  由上图，我们可以发现$\sin(\theta_{max})=\frac{R}{length(c-p)}$。所以：

$$\cos(\theta_{max})=\sqrt{1-\frac{R^2}{length^2(c-p)}}$$

  我们还需要求解所有方向与球体所交的立体角。对于球体上的均匀分布，PDF是$\frac{1}{solid_angle}$。这种情况下，立体角是多少呢？这与上面的 $C$ 有关。根据定义，它是单位球面上的面积，因此积分为：

$$solid\_angle=\int_0^{2\pi}\int_0^{\theta_{max}}\sin(\theta)=2\pi\cdot(1-\cos(\theta_{max}))$$

  最好检查一下上面数学推演得到的结论。我经常代入一些极端值进行检验（谢谢你的教导，Horton先生——我的高中物理老师）。对于半径为0的球体，$\cos(\theta_{max})=1$，公式正确。对于球体表面的切点$p$，$\cos(\theta_{max})=0$，且$2\pi$是半球面积，这也对了。

12.4. 更新球的代码

  球的类需要实现两个PDF相关的函数：

#include "hittable.h"
#include "onb.h"

class sphere : public hittable {
  public:
    ...

    aabb bounding_box() const override { return bbox; }

    double pdf_value(const point3& origin, const vec3& direction) const override {
        // This method only works for stationary spheres.

        hit_record rec;
        if (!this->hit(ray(origin, direction), interval(0.001, infinity), rec))
            return 0;

        auto dist_squared = (center.at(0) - origin).length_squared();
        auto cos_theta_max = std::sqrt(1 - radius*radius/dist_squared);
        auto solid_angle = 2*pi*(1-cos_theta_max);

        return  1 / solid_angle;
    }

    vec3 random(const point3& origin) const override {
        vec3 direction = center.at(0) - origin;
        auto distance_squared = direction.length_squared();
        onb uvw(direction);
        return uvw.transform(random_to_sphere(radius, distance_squared));
    }

  private:
    ...

    static vec3 random_to_sphere(double radius, double distance_squared) {
        auto r1 = random_double();
        auto r2 = random_double();
        auto z = 1 + r2*(std::sqrt(1-radius*radius/distance_squared) - 1);

        auto phi = 2*pi*r1;
        auto x = std::cos(phi) * std::sqrt(1-z*z);
        auto y = std::sin(phi) * std::sqrt(1-z*z);

        return vec3(x, y, z);
    }
};

  我们可以先尝试只采样球体，而不采样光源：

int main() {
    ...

    // Light
    world.add(make_shared<quad>(point3(213,554,227), vec3(130,0,0), vec3(0,0,105), light));

    // Box
    shared_ptr<hittable> box1 = box(point3(0,0,0), point3(165,330,165), white);
    box1 = make_shared<rotate_y>(box1, 15);
    box1 = make_shared<translate>(box1, vec3(265,0,295));
    world.add(box1);

    // Glass Sphere
    auto glass = make_shared<dielectric>(1.5);
    world.add(make_shared<sphere>(point3(190,90,190), 90, glass));

    // Light Sources
    auto empty_material = shared_ptr<material>();
    quad lights(point3(343,554,332), vec3(-130,0,0), vec3(0,0,-105), empty_material);

    ...
}

  这会产生噪点比较多的结果，不过在球体下的焦散很好。它花费的时间是对光源采样的时间的5倍。这是由于射线与玻璃碰撞的开销太大了！（译者注：下面这张图应该是采样了光源的）

12.5. 给Hittable List增加PDF函数

  我们可能应该只对球体和光线进行采样。我们可以通过创建它们的两个分布的混合密度来做到这一点。我们可以在ray_color()函数中通过传递hittable_list并构建混合 PDF 来做到这一点，或者我们可以将PDF函数添加到hittable_list中。我认为二者皆可，不过我还是希望在hittable_list中种增加PDF函数。

class hittable_list : public hittable {
  public:
    ...

    aabb bounding_box() const override { return bbox; }

    double pdf_value(const point3& origin, const vec3& direction) const override {
        auto weight = 1.0 / objects.size();
        auto sum = 0.0;

        for (const auto& object : objects)
            sum += weight * object->pdf_value(origin, direction);

        return sum;
    }

    vec3 random(const point3& origin) const override {
        auto int_size = int(objects.size());
        return objects[random_int(0, int_size-1)]->random(origin);
    }

    ...
};

  我们把需要传递给camera::render()的光源组装到一起：

int main() {
    ...

    // Light Sources
    auto empty_material = shared_ptr<material>();
    hittable_list lights;
    lights.add(
        make_shared<quad>(point3(343,554,332), vec3(-130,0,0), vec3(0,0,-105), empty_material));
    lights.add(make_shared<sphere>(point3(190, 90, 190), 90, empty_material));

    ...
}

  和以前一样，我们得到了一个包含1000个样本的不错的图像：

12.6. 处理表面瑕疵

  一位精明的读者指出，上图中有一些黑点。所有Monte Carlo光线追踪渲染器的主循环都如下：

pixel_color = average(many many samples)

  如果你发现自己在渲染中出现了某种形式的瑕疵，并且这个瑕疵是白色或黑色的——一个“坏”样本似乎杀死了整个像素——那么那个样本可能是一个巨大的数字或一个 NaN（not a number）。我这边似乎每 10-1亿条射线左右出现一次。

  所以做一个大决定：把这个错误扫到地毯下，并且检查 NaN，或者干脆杀死 NaN，希望它以后不会回来咬我们。我总是会选择懒惰的策略，尤其是当我知道和浮点数打交道很困难时。首先是，我们如何检查NaN？我时常记得的一件事情是NaN和自己不相等。基于这一点，我们可以更新write_color()函数来将所有NaN置为0:

void write_color(std::ostream& out, const color& pixel_color) {
    auto r = pixel_color.x();
    auto g = pixel_color.y();
    auto b = pixel_color.z();

    // Replace NaN components with zero.
    if (r != r) r = 0.0;
    if (g != g) g = 0.0;
    if (b != b) b = 0.0;

    // Apply a linear to gamma transform for gamma 2
    r = linear_to_gamma(r);
    g = linear_to_gamma(g);
    b = linear_to_gamma(b);

    // Translate the [0,1] component values to the byte range [0,255].
    static const interval intensity(0.000, 0.999);
    int rbyte = int(256 * intensity.clamp(r));
    int gbyte = int(256 * intensity.clamp(g));
    int bbyte = int(256 * intensity.clamp(b));

    // Write out the pixel color components.
    out << rbyte << ' ' << gbyte << ' ' << bbyte << '\n';
}

  很好，黑色的瑕疵消失了：

13. 往后余生

  本书的目的是介绍在组织基于物理的渲染器的采样方法时，所需考虑的所有小细节。你现在应该能够了解所有这些细节并探索许多不同的潜在路径。

  如果要探索Monte Carlo方法，请查看双向和路径空间方法，例如Metropolis。你的概率空间不会超过立体角，而是位于路径空间上，其中路径是高维空间中的多维点。不要被吓到——如果你能用一个数字数组来描述一个物体，数学家就把它称为所有可能的点数组中的一个点。这不仅仅是为了作秀。一旦你得到了一个像这样简洁的抽象描述，你的代码也会变得干净而简洁。抽象且简洁就是编程的全部意义！

  如果你想制作影片渲染器，请查看工作室和Solid Angle的论文。他们对自己的成果出奇地开放。

  如果你想进行高性能光线追踪，请首先查看Intel和NVIDIA的论文。他们也出乎意料地开放。

  如果要制作基于物理的硬核渲染器，请将渲染器的颜色表示从RGB转换为光谱。我非常喜欢每条光线都具有随机波长，并且程序中的几乎所有RGB都变成了浮点数。这看起来效率低下，但事实并非如此。

  无论你选择哪个方向，都可以添加光泽的BRDF模型。有很多可供选择，每种都有其优点。

  玩的开心。

  Peter Shirley
  Salt Lake City, March, 2016

14. 致谢（非正文）

  很开心在这段时间能够把三本书都翻译完。三本书讲的内容虽然很基础，但是对我来说，也只是有一个印象。最初是想趁着离职之后的这段时间把这些内容看一遍，做一遍，再总结一遍，后来想想与其再总结一遍，不如一边看，一边写，一边翻译，然后可以发表不错的中译版，供后续感兴趣的中文语境的读者阅读和参考。

  在翻译过程中，也参考一些网上其他中译版本，要么残缺，要么就是不准确。不过作为参考已经足矣，也在此感谢前人栽树。而越看到后面，可参考的资料就越少，例如到第三本的时候，中译本寥寥，笔记和总结多一些。这时候就希望我的工作可以弥补这个空缺。

  最后想感谢我的妻子。因为离职空窗期即将结束，我希望在开始新的工作之前把翻译工作完成，所以几乎每天都是在啃书，啃谷歌翻译，还有回忆自己的中学英语。而我的妻子为搬家忙前忙后，把所有东西都收拾整齐，打包装箱，安排所有行程。我时常听见背后她忙碌的声音，但我还是专注在自己的文字和代码工作上，今天刚好是我们领证一周年纪念日，这也是给她的礼物。

译者：寒江雪

2024年1月5日

---

转载请注明来源，欢迎对文章中的引用来源进行考证，欢迎指出任何有错误或不够清晰的表达。可以邮件